Question

若曲线C₁：ρ=2cosθ与曲线C₂：y（y-mx-m）=0有4个不同的交点，则实数m的取值范围是（　　）

• A、（-

  3

  3

  ，

  3

  3

  ）
• B、（-

  3

  3

  ，0）∪（0，

  3

  3

  ）
• C、[-

  3

  3

  ，

  3

  3

  ]
• D、（-∞，-

  3

  3

  ）∪（

  3

  3

  ，+∞）

Answer 1

考点：简单曲线的极坐标方程

专题：坐标系和参数方程

分析：曲线C₁：ρ=2cosθ化为ρ²=2ρcosθ，化为曲线C₁：（x-1）²+y²=1，图象为圆心为（1，0），半径为1的圆；曲线C₂：y=0，或者y-mx-m=0，直线y-mx-m=0恒过定点（-1，0），即曲线C₂图象为x轴与恒过定点（-1，0）的两条直线．结合图形即可得出．

解答： 解：曲线C₁：ρ=2cosθ化为ρ²=2ρcosθ，∴x²+y²=2x．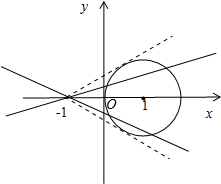
曲线C₁：（x-1）²+y²=1，图象为圆心为（1，0），半径为1的圆；
曲线C₂：y=0，或者y-mx-m=0，直线y-mx-m=0恒过定点（-1，0），即曲线C₂图象为x轴与恒过定点（-1，0）的两条直线．
作图分析：k₁=tan 30°=

3

3

，k₂=-tan 30°=-

3

3

，
又直线l₁（或直线l₂）、x轴与圆共有四个不同的交点，
结合图形可知m=k∈(-∞，-

3

3

)∪(

3

3

，+∞)．
故选：B．

点评：本题考查了极坐标化为直角坐标、直线与圆的位置关系、斜率，考查了推理能力与计算能力，属于中档题．