题目内容
已知函数f(x)=lnx+cosx-(
-
)x的导数为f′(x),且数列{an}满足an+1+an=nf′(
)+3(n∈N*).
(1)若数列{an}是等差数列,求a1的值;(2)当a1=2时,求数列{an}的前n项和Sn;
(3)若对任意n∈N*,都有
≥4成立,求a1的取值范围.
| 6 |
| π |
| 9 |
| 2 |
| π |
| 6 |
(1)若数列{an}是等差数列,求a1的值;(2)当a1=2时,求数列{an}的前n项和Sn;
(3)若对任意n∈N*,都有
| ||
| an+an+1 |
考点:数列与不等式的综合,等差关系的确定,数列的求和
专题:等差数列与等比数列
分析:求出函数的导数,推出an+1+an=nf′(
)+3的具体表达式,
(1)数列{an}是等差数列,利用an+1+an=4n+3,求出a1的值;
(2)利用an+1+an=4n+3,当a1=2时,推出奇数项与偶数项导数等差数列,然后求数列{an}的前n项和Sn;
(3)通过对任意n∈N*,都有
≥4成立,利用n为奇数与n为偶数,通过不等关系式,分别利用函数的最值问题,求a1的取值范围.
| π |
| 6 |
(1)数列{an}是等差数列,利用an+1+an=4n+3,求出a1的值;
(2)利用an+1+an=4n+3,当a1=2时,推出奇数项与偶数项导数等差数列,然后求数列{an}的前n项和Sn;
(3)通过对任意n∈N*,都有
| ||
| an+an+1 |
解答:
解:函数f(x)=lnx+cosx-(
-
)x,
∴f′(x)=
-sinx-
+
,则f′(
)=4,故an+1+an=4n+3
(1)若数列{an}是等差数列,由an+1+an=4n+3得(a1+nd)+[a1+(n-1)d]=4n+3,
解得:d=2,a1=
(2)由an+1+an=4n+3(n∈N*).得an+2+an+1=4n+7两式相减,得an+2-an=4
故数列{a2n-1}是首项为a1,公差为4的等差数列.数列{a2n}是首项为a2,公差为4
的等差数列,
由a2+a1=7,a1=2,得a2=5,所以an=
①当n为奇数是,an=2n,an+1=2n+3.Sn=(a1+a2)+(a3+a4)+…+(a_n-2=7+15+…+(4n-5)+2n=
+2n=
;
②当n为偶数时,Sn=a1+a2+a3+…+an=(a1+a2)+(a3+a4)+…+(an-1+an)=7+15+…+(4n-1)=
;
(3)由(2)知,an=
,
①当n为奇数时,an=2n-2+a1,an+1=2n+5-a1.
由
≥4得2
-14a1≥-8n2+4n-17.
令f(n)=-8n2+4n-17=-8(n-
)2-
,∴f(n)max=f(1)=-21,∴2
-14a1≥-21.解得a≥
或a≤
.
②当n为偶数时,an=2n+3-a1,an+1=2n+a1.
由
≥4得2
-6a1≥-8n2+4n+3.
令g(n)=-8n2+4n+3=-8(n-
)2+
,∴g(n)max=g(2)=-21,∴2
-6a1≥-21解得a1∈R
综上,a1的取值范围是(-∞,
]∪[
,+∞).
| 6 |
| π |
| 9 |
| 2 |
∴f′(x)=
| 1 |
| x |
| 6 |
| π |
| 9 |
| 2 |
| π |
| 6 |
(1)若数列{an}是等差数列,由an+1+an=4n+3得(a1+nd)+[a1+(n-1)d]=4n+3,
解得:d=2,a1=
| 5 |
| 2 |
(2)由an+1+an=4n+3(n∈N*).得an+2+an+1=4n+7两式相减,得an+2-an=4
故数列{a2n-1}是首项为a1,公差为4的等差数列.数列{a2n}是首项为a2,公差为4
的等差数列,
由a2+a1=7,a1=2,得a2=5,所以an=
|
①当n为奇数是,an=2n,an+1=2n+3.Sn=(a1+a2)+(a3+a4)+…+(a_n-2=7+15+…+(4n-5)+2n=
| ||
| 2 |
| 2n2+3n-1 |
| 2 |
②当n为偶数时,Sn=a1+a2+a3+…+an=(a1+a2)+(a3+a4)+…+(an-1+an)=7+15+…+(4n-1)=
| 2n2+3n |
| 2 |
(3)由(2)知,an=
|
①当n为奇数时,an=2n-2+a1,an+1=2n+5-a1.
由
| ||
| an+an+1 |
| a | 2 1 |
令f(n)=-8n2+4n-17=-8(n-
| 1 |
| 4 |
| 33 |
| 2 |
| a | 2 1 |
7+
| ||
| 2 |
7-
| ||
| 2 |
②当n为偶数时,an=2n+3-a1,an+1=2n+a1.
由
| ||
| an+an+1 |
| a | 2 1 |
令g(n)=-8n2+4n+3=-8(n-
| 1 |
| 4 |
| 7 |
| 2 |
| a | 2 1 |
综上,a1的取值范围是(-∞,
7-
| ||
| 2 |
7+
| ||
| 2 |
点评:本题考查数列的综合应用,数列与不等式的求法,考查计算能力,转化思想的应用.

练习册系列答案
相关题目
| ∫ | 2 1 |
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| x3 |
A、ln2+
| ||
B、ln2-
| ||
C、ln2-
| ||
D、ln2-
|
下列函数中,在其定义域内,既是奇函数又是减函数的是( )
A、f(x)=
| ||
B、f(x)=
| ||
| C、f(x)=-x3 | ||
| D、f(x)=2x-2-x |
若两个等差数列{an},{bn}的前n项的和为An,Bn.且
=
,则
=( )
| An |
| Bn |
| 4n+5 |
| 5n-5 |
| a5+a13 |
| b5+b13 |
A、
| ||
B、
| ||
C、
| ||
D、
|
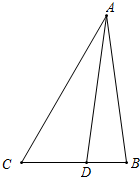 如图,在△ABC中,已知4sin2
如图,在△ABC中,已知4sin2