题目内容
11.已知全集U=R,M={x|y=lg(1-$\frac{2}{x}$)},N={x|y=$\sqrt{x-1}$},则N∩(∁UM)=( )| A. | ∅ | B. | [1,2] | C. | [0,2] | D. | [2,+∞) |
分析 求出两个函数的定义域,可得集合M,N,结合集合的交集,并集,补集运算法则,可得答案.
解答 解:由1-$\frac{2}{x}$>0得:x<0,或x>2,
故∁UM=[0,2],
由x-1≥0得:x≥1,
故N=[1,+∞),
∴N∩(∁UM)=[1,2]
故选:B
点评 本题考查的知识点是集合的交集,并集,补集运算,难度不大,属于基础题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
16.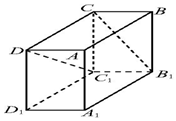 在长方体ABCD-A1B1C1D1中,B1C和C1D与底面所成的角分别为60°和45°,则异面直线B1C和C1D所成角的余弦值为( )
在长方体ABCD-A1B1C1D1中,B1C和C1D与底面所成的角分别为60°和45°,则异面直线B1C和C1D所成角的余弦值为( )
 在长方体ABCD-A1B1C1D1中,B1C和C1D与底面所成的角分别为60°和45°,则异面直线B1C和C1D所成角的余弦值为( )
在长方体ABCD-A1B1C1D1中,B1C和C1D与底面所成的角分别为60°和45°,则异面直线B1C和C1D所成角的余弦值为( )| A. | $\frac{{\sqrt{6}}}{4}$ | B. | $\frac{{\sqrt{6}}}{3}$ | C. | $\frac{{\sqrt{2}}}{6}$ | D. | $\frac{{\sqrt{2}}}{3}$ |
3.定义在R上的偶函数f(x)满足:对任意的x1,x2∈[0,+∞)(x1≠x2),有$\frac{f({x}_{2})-f({x}_{1})}{{x}_{2}-{x}_{1}}<0$.则( )
| A. | f(3)<f(-2)<f(1) | B. | f(1)<f(-2)<f(3) | C. | f(-2)<f(1)<f(3) | D. | f(3)<f(1)<f(-2) |
1.已知一个圆锥的正视图和侧视图都是边长为1的正三角形,则它的俯视图的面积是( )
| A. | π | B. | $\frac{π}{2}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{4}$ |
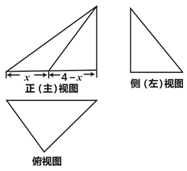 已知三棱锥的外接球的表面积为25π,该三棱锥的三视图如图所示,三个视图的外轮廓都是直角三角形,则其侧视图面积的最大值为3.
已知三棱锥的外接球的表面积为25π,该三棱锥的三视图如图所示,三个视图的外轮廓都是直角三角形,则其侧视图面积的最大值为3.