题目内容
16.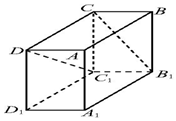 在长方体ABCD-A1B1C1D1中,B1C和C1D与底面所成的角分别为60°和45°,则异面直线B1C和C1D所成角的余弦值为( )
在长方体ABCD-A1B1C1D1中,B1C和C1D与底面所成的角分别为60°和45°,则异面直线B1C和C1D所成角的余弦值为( )| A. | $\frac{{\sqrt{6}}}{4}$ | B. | $\frac{{\sqrt{6}}}{3}$ | C. | $\frac{{\sqrt{2}}}{6}$ | D. | $\frac{{\sqrt{2}}}{3}$ |
分析 利用长方体的性质、线面角的定义、异面直线所成的角的定义即可得出.
解答 解:如图所示: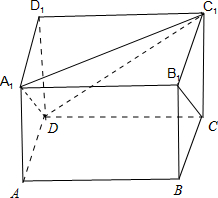
∵B1B⊥平面ABCD,∴∠BCB1是B1C与底面所成角,
∴∠BCB1=60°.
∵C1C⊥底面ABCD,∴∠CDC1是C1D与底面所成的角,
∴∠CDC1=45°.
连接A1D,A1C1,则A1D∥B1C.∴∠A1DC1或其补角为异面直线B1C与C1D所成的角.
不妨设BC=1,则CB1=DA1=2,$B{B}_{1}=C{C}_{1}=\sqrt{3}$=CD,
∴${C}_{1}D=\sqrt{6}$,A1C1=2.
在等腰△A1C1D中,cos∠A1DC1=$\frac{\frac{1}{2}{C}_{1}D}{{A}_{1}D}$=$\frac{\sqrt{6}}{4}$.
故选:A.
点评 熟练掌握长方体的性质、线面角与异面直线所成的角的定义是解题的关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
11.已知全集U=R,M={x|y=lg(1-$\frac{2}{x}$)},N={x|y=$\sqrt{x-1}$},则N∩(∁UM)=( )
| A. | ∅ | B. | [1,2] | C. | [0,2] | D. | [2,+∞) |
1.已知命题p:?x∈R,2x2+2x+$\frac{1}{2}$<0,命题q:?x0∈R,sinx0-cosx0=$\sqrt{2}$,则下列判断中正确的是( )
| A. | p是真命题 | B. | q是假命题 | C. | ¬p是假命题 | D. | ¬q是假命题 |
8.若集合A={x|x2<4},且A∪B=A,则集合B可能是( )
| A. | {1,2} | B. | {x|x<2} | C. | {-1,0,1} | D. | R |
6.函数f(x)的定义域为R,周期为1,当0≤x<1时f(x)=x,若函数f(x)的图象与$g(x)=2{x^2}+\sqrt{k}$的图象只有一个交点,则实数k的取值范围是( )
| A. | $[\frac{1}{64},1]$ | B. | $[\frac{1}{8},1]$ | C. | $(\frac{1}{64},1)$ | D. | $(\frac{1}{8},1)$ |
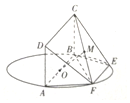 如图,AB为圆O的直径,点E,F在圆O上,AB∥EF,矩形ABCD所在的平面和圆(x-1)2+y2=1所在的平面互相垂直,且AB=2,AD=EF=1,∠BAF=60°.
如图,AB为圆O的直径,点E,F在圆O上,AB∥EF,矩形ABCD所在的平面和圆(x-1)2+y2=1所在的平面互相垂直,且AB=2,AD=EF=1,∠BAF=60°.