题目内容
4．设x1，x2分别是函数y=$\frac{1}{{x}_{1}}$与y=ex，y=1nx交点的横坐标，则x1+2x2的取值范围是（3，+∞）．分析 由题意可得ex1=$\frac{1}{{x}_{1}}$，${e}^{\frac{1}{{x}_{2}}}$=x2，从而可得$\frac{1}{{x}_{1}}$=x2，x2＞1；再由函数的单调性求解．
解答 解：由题意可得，
x1ex1=1，x2logex2=1；
故ex1=$\frac{1}{{x}_{1}}$，${e}^{\frac{1}{{x}_{2}}}$=x2，
又∵y=ex在（0，+∞）上单调递增，
故$\frac{1}{{x}_{1}}$=x2，x2＞1；
故x1+2x2=$\frac{1}{{x}_{2}}$+2x2，
而y=$\frac{1}{{x}_{2}}$+2x2在（1，+∞） 上是增函数，
故$\frac{1}{{x}_{2}}$+2x2＞3；
故答案为：（3，+∞）．
点评 本题考查了方程的根的确定及函数的性质的应用，属于中档题．
练习册系列答案
相关题目
12．在△ABC中，p：△ABC是等边三角形，q：a：b：c=sinB：sinC：sinA，则p是q的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
11．某市根据地理位置划分成了南北两区，为调查该市的一种经济作物A（下简称A作物）的生长状况，用简单随机抽样方法从该市调查了500处A作物种植点，其生长状况如表：
其中生长指数的含义是：2代表“生长良好”，1代表“生长基本良好”，0代表“不良好，但仍有收成”，-1代表“不良好，绝收”．
（Ⅰ）估计该市空气质量差的A作物种植点中，不绝收的种植点所占的比例；
（Ⅱ）能否有99%的把握认为“该市A作物的种植点是否绝收与所在地域有关”？
（Ⅲ）根据（Ⅱ）的结论，能否提供更好的调查方法来估计该市A作物的种植点中，绝收种植点的比例？并说明理由．
附：
${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$．
| 生长指数 | 2 | 1 | 0 | -1 | ||
| 地域 | 南区 | 空气质量好 | 45 | 54 | 26 | 35 |
| 空气质量差 | 7 | 16 | 12 | 5 | ||
| 北区 | 空气质量好 | 70 | 105 | 20 | 25 | |
| 空气质量差 | 19 | 38 | 18 | 5 | ||
（Ⅰ）估计该市空气质量差的A作物种植点中，不绝收的种植点所占的比例；
（Ⅱ）能否有99%的把握认为“该市A作物的种植点是否绝收与所在地域有关”？
（Ⅲ）根据（Ⅱ）的结论，能否提供更好的调查方法来估计该市A作物的种植点中，绝收种植点的比例？并说明理由．
附：
| P（K2≥k） | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
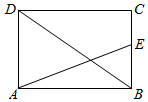
如图，在几何体ABCDEF中，等腰梯形ABCD所在的平面与正方形CDEF所在的平面互相垂直，已知AB∥CD，AB=2BC=4，∠ABC=60°，点M是线段AC的中点．