题目内容
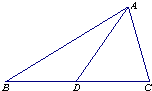 如图,在△ABC中,点D在BC边上,AD=33,sin∠BAD=
如图,在△ABC中,点D在BC边上,AD=33,sin∠BAD=| 5 |
| 13 |
| 3 |
| 5 |
(Ⅰ)求sin∠ABD的值;
(Ⅱ)求△ABD的面积.
考点:正弦定理
专题:解三角形
分析:(Ⅰ)由条件求得cos∠ADB和sin∠ADB、cos∠BAD的值,再根据sin∠ABD=sin(π-∠ADC-∠BAD)=sin(∠ADC+∠BAD),再利用两角和的正弦公式计算求得结果.
(Ⅱ)△ABD中,由正弦定理求得AB=52,根据△ABD的面积为S=
•AB•AD•sin∠BAD,计算求得结果.
(Ⅱ)△ABD中,由正弦定理求得AB=52,根据△ABD的面积为S=
| 1 |
| 2 |
解答:
解:(Ⅰ)如图,在△ABC中,∵cos∠ADC=
,∴cos∠ADB=-
,sin∠ADB=
.
∵sin∠BAD=
,∴cos∠BAD=
.
∴sin∠ABD=sin(π-∠ADC-∠BAD)=sin(∠ADC+∠BAD)
=sin∠ADB•cos∠BAD+cos∠ADB•sin∠BAD=
×
+(-
)×
=
.
(Ⅱ)△ABD中,由正弦定理可得
=
,即
=
,求得AB=52,
故△ABD的面积为S=
•AB•AD•sin∠BAD=
×52×33×
=
.
| 3 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
∵sin∠BAD=
| 5 |
| 13 |
| 12 |
| 13 |
∴sin∠ABD=sin(π-∠ADC-∠BAD)=sin(∠ADC+∠BAD)
=sin∠ADB•cos∠BAD+cos∠ADB•sin∠BAD=
| 4 |
| 5 |
| 12 |
| 13 |
| 3 |
| 5 |
| 5 |
| 13 |
| 33 |
| 65 |
(Ⅱ)△ABD中,由正弦定理可得
| AD |
| sin∠ABD |
| AB |
| sin∠ADB |
| 33 | ||
|
| AB | ||
|
故△ABD的面积为S=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 13 |
| 10 |
| 33 |
点评:本题主要考查同角三角函数的基本关系、诱导公式、两角和的正弦公式、正弦定理的应用,属于基础题.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
 某校运动会开幕式上举行升旗仪式,旗杆正好处在坡度15°的看台的某一列的正前方,从这一列的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,第一排和最后一排的距离为10
某校运动会开幕式上举行升旗仪式,旗杆正好处在坡度15°的看台的某一列的正前方,从这一列的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,第一排和最后一排的距离为10