题目内容
4.在极坐标系中,P是曲线C1:ρ=12sinθ上的动点,Q是曲线C2:ρ=12cos(θ-$\frac{π}{6}$)上的动点,(1)求曲线C1,C2的平面直角坐标方程并说明表示什么曲线;
(2)试求PQ的最大值.
分析 (1)把已知等式两边同时乘ρ,结合公式ρ2=x2+y2,y=ρsinθ求得C1的直角坐标方程;展开两角差的余弦,把已知等式两边同时乘ρ,结合公式ρ2=x2+y2,x=ρcosx,y=ρsinθ求得C2的直角坐标方程;
(2)画出图形,数形结合得答案.
解答 解:(1)以极点O为原点,极轴为x轴建立直角坐标系xOy.
由ρ=12sinθ,得ρ2=12ρsinθ,得x2+y2=12y,即x2+(y-6)2=36,
∴C1表示圆心为(0,6),半径为6的圆.
由ρ=12cos(θ-$\frac{π}{6}$),得$ρ=12(\frac{\sqrt{3}}{2}cosθ+\frac{1}{2}sinθ)$
=$6\sqrt{3}cosθ+6sinθ$,
∴${ρ}^{2}=6\sqrt{3}ρcosθ+6ρsinθ$,即${x}^{2}+{y}^{2}-6\sqrt{3}x-6y=0$,
则(x-3$\sqrt{3}$)2+(y-3)2=36,
∴C2表示以(3$\sqrt{3}$,3)为圆心,6为半径的圆.
(2)由圆的位置关系可知,当P、Q所在直线为连心线所在直线时,PQ长度可取最大值,且最大值为$\sqrt{(3\sqrt{3})^{2}+{3}^{2}}$+6+6=18.
点评 本题考查简单曲线的极坐标方程,考查两圆的位置关系,体现了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
9.参数方程为$\left\{{\begin{array}{l}{x=-3+2cosθ}\\{y=4+2sinθ}\end{array}}\right.(θ为参数)$,表示的曲线是( )
| A. | 圆 | B. | 椭圆 | C. | 双曲线 | D. | 直线 |
16.设向量$\overrightarrow{BA}$=(3,2),$\overrightarrow{BC}$=(3,-4),$\overrightarrow{AD}$=(0,2),则( )
| A. | $\overrightarrow{AB}∥\overrightarrow{BC}$ | B. | $\overrightarrow{AB}∥\overrightarrow{AD}$ | C. | $\overrightarrow{BC}∥\overrightarrow{AC}$ | D. | $\overrightarrow{AC}∥\overrightarrow{AD}$ |
13.执行如图所示的程序框图,若输出的结果是8,则判断框内m的取值范围是( )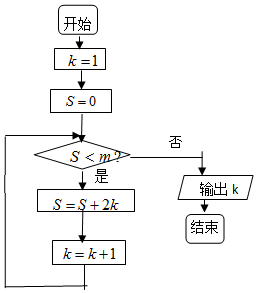

| A. | (42,56] | B. | (20,30] | C. | (30,42] | D. | (20,42) |
14.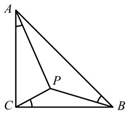 如图,在等腰直角三角形ABC中,∠C是直角,P是三角形内部一点,且∠CAP=∠BCP=∠ABP=α,则tanα的值等于( )
如图,在等腰直角三角形ABC中,∠C是直角,P是三角形内部一点,且∠CAP=∠BCP=∠ABP=α,则tanα的值等于( )
 如图,在等腰直角三角形ABC中,∠C是直角,P是三角形内部一点,且∠CAP=∠BCP=∠ABP=α,则tanα的值等于( )
如图,在等腰直角三角形ABC中,∠C是直角,P是三角形内部一点,且∠CAP=∠BCP=∠ABP=α,则tanα的值等于( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |