题目内容
15.设f(x)=$\frac{{-{2^x}+m}}{{{2^{x+1}}+n}}$(m>0,n>0).(1)若f(x)是奇函数,求m与n的值;
(2)在(1)的条件下,求不等式$f[{f(x)}]+f(\frac{1}{4})<0$的解集.
分析 (1)由f(x)是奇函数,可得f(0)=0,求得m=1.再根据f(-1)=-f(1),求得n=2,检验满足条件.
(2)利用导数可得f(x)是R上单调减函数.由$f[{f(x)}]+f(\frac{1}{4})<0$,得$f[{f(x)}]<f(-\frac{1}{4})$,即$f(x)>-\frac{1}{4}$,从而求得2x<3,解得x的范围.
解答 解:(1)f(x)是奇函数,f(-x)=-f(x),依题意,f(x)的定义域是R,
所以f(0)=0,即$\frac{-1+m}{2+n}=0$,解得m=1,
又f(-1)=-f(1),即$\frac{{-\frac{1}{2}+1}}{1+n}=\frac{-2+1}{4+a}$,解得n=2,
所以,m=1,n=2.经检验,满足f(-x)=-f(x).
(2)由(1)可知$f(x)=\frac{{-{2^x}+1}}{{{2^{x+1}}+2}}=-\frac{1}{2}+\frac{1}{{{2^x}+1}}$,再根据 ${f^'}(x)=\frac{{-{2^x}ln2}}{{{{({2^x}+1)}^2}}}<0$,
可得f(x)是R上单调减函数.
由$f[{f(x)}]+f(\frac{1}{4})<0$,得$f[{f(x)}]<f(-\frac{1}{4})$
即$f(x)>-\frac{1}{4}$,从而$-\frac{1}{2}+\frac{1}{{{2^x}+1}}>-\frac{1}{4}$,得2x<3,解得x<log23,
即$f[{f(x)}]+f(\frac{1}{4})<0$的解集为{x{x<log23}.
点评 本题主要考查函数的单调性和奇偶性的应用,利用导数研究函数的单调性,属于中档题.

 期末集结号系列答案
期末集结号系列答案m(件)与时间t(天)的关系如表所示.
| 时间t/天 | 1 | 3 | 6 | 10 | 36 | … |
| 日销售量 m/件 | 94 | 90 | 84 | 76 | 24 | … |
(1)认真分析表格中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些 数据的m(件)与t(天)的关系式.
(2)试预测未来40天中哪一天的日销售利润最大,最大利润是多少?
(3)在实际销售的前20天中,该公司决定每销售1件商品就捐赠a元利润(a<4)给希望工程.公司通过销售记录发现,前20天中,每天扣除捐赠后的日销售利润随时间t(天)的增大而增大,求a的取值范围.
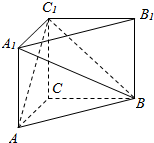 如图:在直三棱柱ABC-A1B1C1中,AA1=BC=AC=2,AC⊥BC.
如图:在直三棱柱ABC-A1B1C1中,AA1=BC=AC=2,AC⊥BC. 一几何体的三视图如图所示,其中侧(左)视图和俯视图都是腰长为2的等腰直角三角形,则此几何体体积的大小为( )
一几何体的三视图如图所示,其中侧(左)视图和俯视图都是腰长为2的等腰直角三角形,则此几何体体积的大小为( )