题目内容
3.设三棱柱ABC-A1B1C1为正三棱柱,底面边长及侧棱长均为a,E、F分别是AA1,CC1的中点,求几何体B-EFB1的体积.分析 利用分割法,取BB1的中点D,连接DE,DF,三棱锥B-EFB1可分为两个体积相等的三棱锥B1-DEF和B-DEF,即可得出结论.
解答  解:取BB1的中点D,连接DE,DF,则△DEF≌△BAC,
解:取BB1的中点D,连接DE,DF,则△DEF≌△BAC,
∴三棱锥B-EFB1可分为两个体积相等的三棱锥B1-DEF和B-DEF,
∴几何体B-EFB1的体积V=$\frac{1}{3}{S}_{△DEF}•({B}_{1}D+BD)$=$\frac{1}{3}×\frac{\sqrt{3}}{4}{a}^{2}•a$=$\frac{\sqrt{3}}{12}{a}^{3}$.
点评 本题考查几何体B-EFB1的体积.利用分割法,三棱锥B-EFB1可分为两个体积相等的三棱锥B1-DEF和B-DEF是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.一艘船以20km/h的速度向正北航行,船在A处看见灯塔B在船的东北方向,1h后船在C处看见灯塔B在船的北偏东75°的方向上,这时船与灯塔的距离BC等于( )
| A. | 20$\sqrt{2}$ | B. | 20 | C. | 20$\sqrt{3}$ | D. | 10$\sqrt{2}$ |
18.一个袋中装有1个红球,1个黄球和两个小立方体,两个球除了颜色外都相同,两个立方体中一个每一面都涂红,另一个每个面都涂黄,除此以外它们都相同,从袋中摸出一个球和一个立方体,下面说法中错误的是( )
| A. | 所有可能出现的结果有四种 | B. | 摸出2个都是红的概率为$\frac{1}{4}$ | ||
| C. | 摸出2个都是黄的概率为$\frac{1}{4}$ | D. | 摸出一红一黄的概率也是$\frac{1}{4}$ |
12.平行六面体ABCD-A1B1C1D1中,AB=5,AD=3,AA1=7,∠CBA=120°,∠BAA1=∠DAA1=45°,则AC1的长等于( )
| A. | 83 | B. | $\sqrt{83}$ | C. | 98$+56\sqrt{2}$ | D. | $\sqrt{98+56\sqrt{2}}$ |
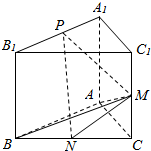 如图,已知三棱柱ABC-A1B1C1的侧面与底面垂直,AA1=AB=AC=1,AB⊥AC,M、N、P分别是CC1、BC、A1B1的中点.
如图,已知三棱柱ABC-A1B1C1的侧面与底面垂直,AA1=AB=AC=1,AB⊥AC,M、N、P分别是CC1、BC、A1B1的中点.