题目内容
6.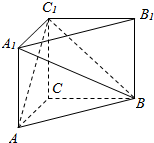 如图:在直三棱柱ABC-A1B1C1中,AA1=BC=AC=2,AC⊥BC.
如图:在直三棱柱ABC-A1B1C1中,AA1=BC=AC=2,AC⊥BC.(1)求多面体ABC-A1C1的体积;
(2)异面直线A1B与AC1所成角的大小.
分析 (1)多面体ABC-A1C1的体积V=${V}_{{C}_{1}-ABC}+{V}_{B-A{A}_{1}{C}_{1}}$,由此能求出结果.
(2)以C为原点,CA为x轴,CB为y轴,CC1为z轴,建立空间直角坐标系,利用向量法能求出异面直线A1B与AC1所成角的大小.
解答  解:(1)∵在直三棱柱ABC-A1B1C1中,AA1=BC=AC=2,AC⊥BC,
解:(1)∵在直三棱柱ABC-A1B1C1中,AA1=BC=AC=2,AC⊥BC,
∴CC1⊥平面ABC,BC⊥平面AA1C1,
∵S△ABC=$\frac{1}{2}×AC×BC$=$\frac{1}{2}×2×2=2$,
${S}_{△A{A}_{1}{C}_{1}}$=$\frac{1}{2}×A{A}_{1}×{A}_{1}{C}_{1}$=$\frac{1}{2}×2×2$=2,
CC1=2,BC=2,
∴多面体ABC-A1C1的体积:
V=${V}_{{C}_{1}-ABC}+{V}_{B-A{A}_{1}{C}_{1}}$
=$\frac{1}{3}×C{C}_{1}×{S}_{△ABC}$+$\frac{1}{3}×BC×{S}_{△A{A}_{1}{C}_{1}}$
=$\frac{1}{3}×2×2+\frac{1}{3}×2×2$
=$\frac{8}{3}$.
(2)以C为原点,CA为x轴,CB为y轴,CC1为z轴,建立空间直角坐标系,
则A1(2,0,2),B(0,2,0),A(2,0,0),C1(0,0,2),
$\overrightarrow{{A}_{1}B}$=(-2,2,-2),$\overrightarrow{A{C}_{1}}$=(-2,0,2),
设异面直线A1B与AC1所成角的大小为θ,
则cosθ=|cos<$\overrightarrow{{A}_{1}B}$,$\overrightarrow{A{C}_{1}}$>|=|$\frac{\overrightarrow{{A}_{1}B}•\overrightarrow{A{C}_{1}}}{|\overrightarrow{{A}_{1}B}|•|\overrightarrow{A{C}_{1}}|}$|=0,
∴异面直线A1B与AC1所成角的大小为$\frac{π}{2}$.
点评 本题考查多面体的体积的求法,考查异面直线所成角的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

| A. | $\frac{64\sqrt{2}}{3}$π | B. | $\frac{32\sqrt{2}}{3}$π | C. | $\frac{8\sqrt{2}}{3}$π | D. | 8π |
| A. | 所有可能出现的结果有四种 | B. | 摸出2个都是红的概率为$\frac{1}{4}$ | ||
| C. | 摸出2个都是黄的概率为$\frac{1}{4}$ | D. | 摸出一红一黄的概率也是$\frac{1}{4}$ |
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
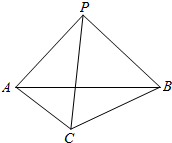 如图,在三棱锥P-ABC中,PA=PB=$\sqrt{6}$,PA⊥PB,AB⊥BC,∠BAC=30°,平面PAB⊥平面ABC.
如图,在三棱锥P-ABC中,PA=PB=$\sqrt{6}$,PA⊥PB,AB⊥BC,∠BAC=30°,平面PAB⊥平面ABC.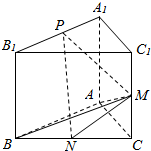 如图,已知三棱柱ABC-A1B1C1的侧面与底面垂直,AA1=AB=AC=1,AB⊥AC,M、N、P分别是CC1、BC、A1B1的中点.
如图,已知三棱柱ABC-A1B1C1的侧面与底面垂直,AA1=AB=AC=1,AB⊥AC,M、N、P分别是CC1、BC、A1B1的中点.