题目内容
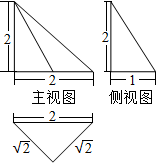
7．
一几何体的三视图如图所示，其中侧（左）视图和俯视图都是腰长为2的等腰直角三角形，则此几何体体积的大小为（ ）| A． | 3 | B． | 4 | C． | 1 | D． | 2 |
分析 由已知中的三视力可得该几何体是一个三棱锥，利用等积法，转化三棱锥的底面和高，再计算出底面面积和高，代入锥体体积公式，可得答案．
解答 解：由已知中的三视力可得该几何体是一个三棱锥，其直观图如下所示：
由AA′∥BC可得：
棱锥A-BCD的体积等于棱锥A′-BCD的体积，等于棱锥B-A′CD的体积，
故V=$\frac{1}{3}$×（2×2-2×$\frac{1}{2}$×1×2-$\frac{1}{2}$×1×1）×2=1，
故选：C
点评 本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．
练习册系列答案
寒假乐园北京教育出版社系列答案
相关题目
17．如图是一个空间几何体的三视图，则该几体体的外接球的体积是（ ）
| A． | $\frac{64\sqrt{2}}{3}$π | B． | $\frac{32\sqrt{2}}{3}$π | C． | $\frac{8\sqrt{2}}{3}$π | D． | 8π |
18．一个袋中装有1个红球，1个黄球和两个小立方体，两个球除了颜色外都相同，两个立方体中一个每一面都涂红，另一个每个面都涂黄，除此以外它们都相同，从袋中摸出一个球和一个立方体，下面说法中错误的是（ ）
| A． | 所有可能出现的结果有四种 | B． | 摸出2个都是红的概率为$\frac{1}{4}$ | ||
| C． | 摸出2个都是黄的概率为$\frac{1}{4}$ | D． | 摸出一红一黄的概率也是$\frac{1}{4}$ |
2．
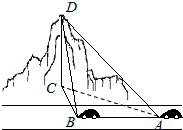如图，有一辆汽车在一条水平的公路上向正西行驶，汽车在A点测得公路北侧山顶D的仰角为30°，汽车行驶300m后到达B点测得山顶D恰好在正北方，且仰角为45°，则山的高度CD为（ ）
如图，有一辆汽车在一条水平的公路上向正西行驶，汽车在A点测得公路北侧山顶D的仰角为30°，汽车行驶300m后到达B点测得山顶D恰好在正北方，且仰角为45°，则山的高度CD为（ ）| A． | 150$\sqrt{2}$ | B． | 150$\sqrt{3}$ | C． | 300$\sqrt{2}$ | D． | 300$\sqrt{3}$ |
12．平行六面体ABCD-A1B1C1D1中，AB=5，AD=3，AA1=7，∠CBA=120°，∠BAA1=∠DAA1=45°，则AC1的长等于（ ）
| A． | 83 | B． | $\sqrt{83}$ | C． | 98$+56\sqrt{2}$ | D． | $\sqrt{98+56\sqrt{2}}$ |
19．已知函数f（x）=$\left\{\begin{array}{l}{（4a-3）x+5-4a（x＜1）}\\{lo{g}_{a}（x-\frac{1}{2}）（x≥1）}\end{array}\right.$是R上的减函数，那么a的取值范围是（ ）
| A． | （0，$\frac{\sqrt{2}}{2}$] | B． | （0，$\frac{3}{4}$] | C． | [$\frac{\sqrt{2}}{2}$，$\frac{3}{4}$] | D． | （$\frac{3}{4}$，1） |
16．某班的课桌分4个大组摆放，每大组课桌数相同，甲、乙均为该班学生，则甲、乙两人的课桌在同一大组的概率是（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{3}{4}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{5}$ |
17．游客从某旅游景区的景点A处至景点C处有两条线路，线路1是从A沿直线步行到C，线路2是先从A沿直线步行到景点B处，然后从B沿直线步行道C，现有甲乙两位游客从A处同时出发匀速步行，甲的速度是乙的速度的$\frac{11}{9}$倍，甲走线路2，乙走线路1，最后他们同时到达C处，经测量，AB=1040m，BC=500m，则sin∠BAC等于（ ）
| A． | $\frac{5}{13}$ | B． | $\frac{3}{5}$ | C． | $\frac{3}{8}$ | D． | $\frac{7}{24}$ |