题目内容
20.已知f(log2x)=ax2-2x+1-a,a∈R.(1)求f(x)的解析式;
(2)解关于x的方程f(x)=(a-1)•4x.
分析 (1)由解析式令log2x=t即x=2t,代入解析式化简求出f(t),将t化为x可得f(x)的解析式;
(2)由(1)化简f(x)=(a-1)•4x,根据指数函数的性质分类讨论,分别由指对互化的式子求出x的表达式.
解答 解:(1)令log2x=t即x=2t,则f(t)=a•(2t)2-2•2t+1-a
即f(x)=a•22x-2•2x+1-a,x∈R
(2)由f(x)=(a-1)•4x得:a•22x-2•2x+1-a=(a-1)•4x,
化简得,22x-2•2x+1-a=0,即(2x-1)2=a,
当a<0时,方程无解;
当a≥0时,解得${2^x}=1±\sqrt{a}$,
所以若0≤a<1,则$x={log_2}(1±\sqrt{a})$,
若a≥1,则$x={log_2}(1+\sqrt{a})$.
点评 本题考查利用换元法求函数的解析式,指对互化、指数函数的性质的应用,考查分类讨论思想,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.如图在边长为1的正方形网格中用粗线画出了某个多面体的三视图,则该多面体的表面积为( )
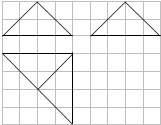

| A. | 8+12$\sqrt{2}$ | B. | 16+24$\sqrt{2}$ | C. | $\frac{1}{3}(8+12\sqrt{2})$ | D. | 4+6$\sqrt{2}$ |
12.平行六面体ABCD-A1B1C1D1中,AB=5,AD=3,AA1=7,∠CBA=120°,∠BAA1=∠DAA1=45°,则AC1的长等于( )
| A. | 83 | B. | $\sqrt{83}$ | C. | 98$+56\sqrt{2}$ | D. | $\sqrt{98+56\sqrt{2}}$ |
9.某空间几何体的三视图如图所示,则此几何体的体积为( )
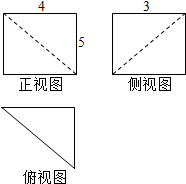

| A. | 10 | B. | 15 | C. | 20 | D. | 30 |
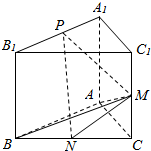 如图,已知三棱柱ABC-A1B1C1的侧面与底面垂直,AA1=AB=AC=1,AB⊥AC,M、N、P分别是CC1、BC、A1B1的中点.
如图,已知三棱柱ABC-A1B1C1的侧面与底面垂直,AA1=AB=AC=1,AB⊥AC,M、N、P分别是CC1、BC、A1B1的中点.