题目内容
8.已知f(x)=4x3-6x2+m(m为常数)在[-2,1]上有最大值5,那么此函数在[-2,1]上的最小值是( )| A. | 3 | B. | -49 | C. | -52 | D. | -51 |
分析 先求导数,根据单调性研究函数的极值点,在开区间(-2,1)上只有一极大值则就是最大值,从而求出m,通过比较两个端点-2和1的函数值的大小从而确定出最小值,得到结论.
解答 解:∵f′(x)=12x2-12x=12x(x-1),
令f′(x)>0,解得:x<0,令f′(x)<0,解得:x>0,
∴f(x)在(-2,0)上为增函数,在(0,1)上为减函数,
∴当x=0时,f(x)=m最大,
∴m=5,从而f(-2)=-51,f(1)=3.
∴最小值为-51.
故选:D.
点评 本题考查了利用导数求闭区间上函数的最值,求函数在闭区间[a,b]上的最大值与最小值是通过比较函数在(a,b)内所有极值与端点函数f(a),f(b) 比较而得到的,属于基础题.

练习册系列答案
相关题目
18.已知点F是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点,过F点作双曲线的一条渐近线垂线,垂足为A,交另一条渐近线于B,若A点恰好为BF的中点,则双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
19.为了得到函数$y=4sin(2x+\frac{π}{5}),x∈R$的图象,只需把函数$y=4sin(x+\frac{π}{5}),x∈R$的图象上所有点的( )
| A. | 横坐标伸长到原来的2倍,纵坐标不变 | |
| B. | 纵坐标伸长到原来的2倍,横坐标不变 | |
| C. | 横坐标伸长到原来的$\frac{1}{2}$倍,纵坐标不变 | |
| D. | 纵坐标伸长到原来的$\frac{1}{2}$倍,横坐标不变 |
16.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的体积为( )


| A. | 32+8π | B. | 32+$\frac{8π}{3}$ | C. | 16+$\frac{8π}{3}$ | D. | 16+8π |
3.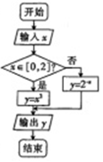 如图是函数y=f(x)求值的程序框图,若输出函数y=f(x)的值域为[4,8],则输入函数y=f(x)的定义域不可能为( )
如图是函数y=f(x)求值的程序框图,若输出函数y=f(x)的值域为[4,8],则输入函数y=f(x)的定义域不可能为( )
 如图是函数y=f(x)求值的程序框图,若输出函数y=f(x)的值域为[4,8],则输入函数y=f(x)的定义域不可能为( )
如图是函数y=f(x)求值的程序框图,若输出函数y=f(x)的值域为[4,8],则输入函数y=f(x)的定义域不可能为( )| A. | [-3,-2] | B. | [-3,-2)∪{2} | C. | [-3,2] | D. | [-3,-2]∪{2} |
20.设函数$f(x)=\left\{\begin{array}{l}2{e^{x-1}},x<2\\{log_3}({{x^2}-1}),x≥2\end{array}\right.$,则f(f(2))的值为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
17.抛物线y2=4x的焦点到双曲线x2-$\frac{{y}^{2}}{{b}^{2}}$=1的一条渐近线的距离是$\frac{\sqrt{3}}{2}$,则双曲线的虚轴长是( )
| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 3 | D. | 6 |