��Ŀ����
13�������������⣺��������PΪ��$\frac{1}{x-1}��0$����VP��$\frac{1}{x-1}��0$��
����sin ��+cos ��=$\frac{1}{2}$����sin2��=-$\frac{3}{4}$��
�����������������ͬ��ƽ�棬m��ֱ����m?������m�Φ¡��ǡ����Φ¡��ı�Ҫ���������
�ܶ�����R�ϵ��溯��f��x������f��x+2��=-f��x������f��x��=0��[0��4]����������������
������ȷ�����Тڢۢܣ�����������ȷ����ı�ţ���
���� �ٸ��ݷ�p��������жϣ�
�ڸ��ݱ��ǹ�ʽ����ɵã�
����ƽ��ƽ�е������жϼ��ɣ�
�ܸ����溯���������жϣ�
��� �⣺��������PΪ��$\frac{1}{x-1}��0$�����x��1����VPΪx��1����$\frac{1}{x-1}��0$�Ľ⼯Ϊx��1���ʴ���
����sin ��+cos ��=$\frac{1}{2}$����sin2��=2sin��cos��=$\frac{1}{4}$-1=-$\frac{3}{4}$������ȷ��
�����������������ͬ��ƽ�棬m��ֱ����m?������m�Φ¡��Ʋ��������Φ¡�������֮�����Ƴ������DZ�Ҫ���������������ȷ��
�ܶ�����R�ϵ��溯��f��x������f��x+2��=-f��x������֪f��0��=0��f��2��=0��f��4��=0����f��x��=0��[0��4]��������������������ȷ��
�ʴ�Ϊ�ڢۢܣ�
���� �����˷�p���⣬���ǹ�ʽ��ƽ��ƽ�е����ʺͺ�������ż�ԣ����ڻ������ͣ�Ӧ�������գ�

��ϰ��ϵ�д�
�����Ŀ
1��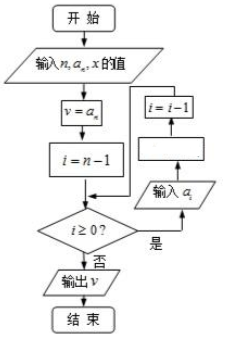 �ҹ�����ʱ�ڵ���ѧ���ؾ���������������������¡�������˼������ʽf��x��=anxn+an-1xn-1+��+a1x+a0��ֵ���ؾ����㷨������f��x����д��������ʽ��f��x��=��������anx+an-1��x+an-2��x+��+a1��x+a0�����ȼ������ڲ�һ�ζ���ʽ��ֵ��Ȼ����������������һ�ζ���ʽ��ֵ�������㷨�������DZȽ��Ƚ����㷨�����ؾ����㷨�ó����ͼ��ʾ��ͼ�����ڿհ�ִ�п���Ӧ���루������
�ҹ�����ʱ�ڵ���ѧ���ؾ���������������������¡�������˼������ʽf��x��=anxn+an-1xn-1+��+a1x+a0��ֵ���ؾ����㷨������f��x����д��������ʽ��f��x��=��������anx+an-1��x+an-2��x+��+a1��x+a0�����ȼ������ڲ�һ�ζ���ʽ��ֵ��Ȼ����������������һ�ζ���ʽ��ֵ�������㷨�������DZȽ��Ƚ����㷨�����ؾ����㷨�ó����ͼ��ʾ��ͼ�����ڿհ�ִ�п���Ӧ���루������
 �ҹ�����ʱ�ڵ���ѧ���ؾ���������������������¡�������˼������ʽf��x��=anxn+an-1xn-1+��+a1x+a0��ֵ���ؾ����㷨������f��x����д��������ʽ��f��x��=��������anx+an-1��x+an-2��x+��+a1��x+a0�����ȼ������ڲ�һ�ζ���ʽ��ֵ��Ȼ����������������һ�ζ���ʽ��ֵ�������㷨�������DZȽ��Ƚ����㷨�����ؾ����㷨�ó����ͼ��ʾ��ͼ�����ڿհ�ִ�п���Ӧ���루������
�ҹ�����ʱ�ڵ���ѧ���ؾ���������������������¡�������˼������ʽf��x��=anxn+an-1xn-1+��+a1x+a0��ֵ���ؾ����㷨������f��x����д��������ʽ��f��x��=��������anx+an-1��x+an-2��x+��+a1��x+a0�����ȼ������ڲ�һ�ζ���ʽ��ֵ��Ȼ����������������һ�ζ���ʽ��ֵ�������㷨�������DZȽ��Ƚ����㷨�����ؾ����㷨�ó����ͼ��ʾ��ͼ�����ڿհ�ִ�п���Ӧ���루������| A�� | v=vx+ai | B�� | v=v��x+ai�� | C�� | v=aix+v | D�� | v=ai��x+v�� |
8����֪f��x��=4x3-6x2+m��mΪ��������[-2��1]�������ֵ5����ô�˺�����[-2��1]�ϵ���Сֵ�ǣ�������
| A�� | 3 | B�� | -49 | C�� | -52 | D�� | -51 |
18��ij�����������ͼ��ͼ��ʾ���������Ϊ��������
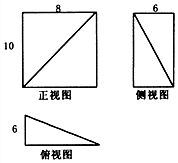

| A�� | 80 | B�� | 160 | C�� | 240 | D�� | 480 |
5��ִ����ͼ��ʾ�ij����ͼ��������p=2017�������i��ֵΪ��������
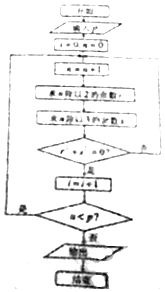

| A�� | 335 | B�� | 336 | C�� | 337 | D�� | 338 |