题目内容
17.设函数f(x)=(x+b)lnx,已知曲线y=f(x)在点(1,f(1))处的切线与直线x+2y=0垂直.(Ⅰ) 求b的值.
(Ⅱ) 若函数$g(x)={e^x}(\frac{f(x)}{x+1}-a)(a≠0)$,且g(x)在区间(0,+∞)上是单调函数,求实数a的取值范围.
分析 (Ⅰ)根据切线的斜率,求出b的值即可;
(Ⅱ)求出g(x)的导数,问题a≥$\frac{1}{x}$+ln x,令h(x)=$\frac{1}{x}$+ln x(x>0),根据函数的单调性求出a的范围即可.
解答 解:(Ⅰ)由题意知,曲线y=f(x)在点(1,f(1))处的切线斜率为2,所以f′(1)=2,-------(2分)
又f′(x)=ln x+$\frac{b}{x}$+1,即ln 1+b+1=2,所以b=1.---------------------------------(4分)
(Ⅱ)由(Ⅰ)知 g(x)=${e^x}(\frac{f(x)}{x+1}-a)$=exln x-aex
所以 g′(x)=($\frac{1}{x}$-a+ln x)ex(x>0),----------------------------------------------------(6分)
若g(x)在(0,+∞)上为单调递减函数,则g′(x)≤0在(0,+∞)上恒成立,
即$\frac{1}{x}$-a+ln x≤0,所以a≥$\frac{1}{x}$+ln x.-----------------------------------------------------(8分)
令h(x)=$\frac{1}{x}$+ln x(x>0),则h′(x)=-$\frac{1}{x2}$+$\frac{1}{x}$=$\frac{x-1}{x2}$
由h′(x)>0,得x>1,h′(x)<0,得0<x<1,
故函数h(x)在(0,1]上是减函数,在[1,+∞)上是增函数,
则$\frac{1}{x}$+ln x→∞,h(x)无最大值,g′(x)≤0在(0,+∞)上不恒成立,
故g(x)在(0,+∞)不可能是单调减函数.------------------------------------------------------(10分)
若g(x)在(0,+∞)上为单调递增函数,则g′(x)≥0在(0,+∞)上恒成立,
即$\frac{1}{x}$-a+ln x≥0,所以a≤$\frac{1}{x}$+ln x,由前面推理知,h(x)=$\frac{1}{x}$+ln x的最小值为1,
∴a≤1,故a的取值范围是(-∞,1].-------------------------------------------------------(12分)
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及函数恒成立问题,是一道中档题.

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案| A. | $3\sqrt{2}$ | B. | 4 | C. | $\sqrt{34}$ | D. | 5 |
| A. | 5 | B. | 4 | C. | $\sqrt{15}$ | D. | $\sqrt{10}$ |
| 分组 | 频数 | 频率 |
| [50,60) | 5 | 0.05 |
| [60,70) | a | 0.20 |
| [70,80) | 35 | b |
| [80,90) | 25 | 0.25 |
| [90,100) | 15 | 0.15 |
| 合计 | 100 | 1.00 |
(Ⅱ)按频率分布表中的成绩分组,采用分层抽样抽取20人参加学校的“我爱国学”宣传活动,求其中优秀生的人数;
(Ⅲ)在第(Ⅱ)问抽取的优秀生中指派2名学生担任负责人,求至少一人的成绩在[90,100]的概率.

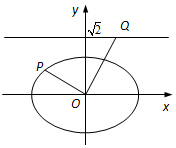 如图,在平面直角坐标系xOy中,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,焦点到相应准线的距离为1.
如图,在平面直角坐标系xOy中,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,焦点到相应准线的距离为1.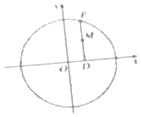 如图,在圆x2+y2=9上任取一点P,过点P作x轴的垂线PD,D为垂足,点M满足$\overrightarrow{DM}=\frac{2}{3}\overrightarrow{DP}$;当点P在圆x2+y2=9上运动时,点M的轨迹为E.
如图,在圆x2+y2=9上任取一点P,过点P作x轴的垂线PD,D为垂足,点M满足$\overrightarrow{DM}=\frac{2}{3}\overrightarrow{DP}$;当点P在圆x2+y2=9上运动时,点M的轨迹为E.