题目内容
18.已知函数g(x)=$\frac{2}{x}-alnx({a∈R}),f(x)={x^2}$+g(x).(1)试判断g(x)的单调性;
(2)若f(x)在区间(0,1)上有极值,求实数a的取值范围;
(3)当a>0时,若f(x)有唯一的零点x0,试求[x0]的值.(注:[x]为取整函数,表示不超过x的最大整数,如[0.3]=0,[2.6]=2,[-1.4]=-2;以下数据供参考:ln2=0.6931,ln3=1.099,ln5=1.609,ln7=1.946)
分析 (1)求出g(x)的导数,讨论当a≥0时,当a<0时,由导数大于0,可得增区间;导数小于0,可得减区间,注意定义域;
(2)求出f(x)的导数,令h(x)=2x3-ax-2,x∈(0,+∞),求出导数,讨论a的符号,判断单调性,即可得到所求a的范围;
(3)由(2)可知:f(1)=3知x∈(0,1)时,f(x)>0,则x0>1,讨论f(x)在x>1的单调性,再由零点的定义和极值点的定义,可得x0的方程,构造函数$t(x)=2lnx-1-\frac{3}{{{x^3}-1}}(x>1)$,判断单调性,由零点存在性定理知 t(2)<0,t(3)>0,即可得到所求值.
解答 解:(1)$g(x)=\frac{2}{x}-alnx(x>0)$,$g'(x)=-\frac{2}{x^2}-\frac{a}{x}=-\frac{ax+2}{x^2}$
①当a≥0时,g'(x)<0,∴函数g(x)在区间(0,+∞)上单调递减;
②当a<0时,由g'(x)=0,解得$x=-\frac{2}{a}$,
当$x∈(0,-\frac{2}{a})$时,g'(x)<0,此时函数g(x)单调递减;
当$x∈(-\frac{2}{a},+∞)$时,g'(x)>0,此时函数g(x)单调递增. …(3分)
(2)f(x)=x2+g(x),其定义域为(0,+∞).
$f'(x)=2x+g'(x)=\frac{{2{x^3}-ax-2}}{x^2}$,…(4分)
令h(x)=2x3-ax-2,x∈(0,+∞),h'(x)=6x2-a,
当a<0时,h'(x)>0恒成立,∴h(x)在(0,+∞)上为增函数,
又h(0)=-2<0,h(1)=-a>0,
∴函数h(x)在(0,1)内至少存在一个变号零点x0,且x0也是f'(x)的变号零点,
此时f(x)在区间(0,1)内有极值. …(5分)
当a≥0时,h(x)=2(x3-1)-ax<0,即x∈(0,1)时,f'(x)<0恒成立,
∴函数f(x)在(0,1)单调递减,此时函数f(x)无极值 …(6分)
综上可得:f(x)在区间(0,1)内有极值时实数a的取值范围是(-∞,0);…(7分)
(3)∵a>0时,函数f(x)的定义域为(0,+∞)
由(2)可知:f(1)=3知x∈(0,1)时,f(x)>0,∴x0>1.
又f(x)在区间(1,+∞)上只有一个极小值点记为x1,
且x∈(1,x1)时,f'(x)<0,函数f(x)单调递减,
x∈(x1,+∞)时,f'(x)>0,函数f(x)单调递增,
由题意可知:x1即为x0. …(9分)
∴$\left\{{\begin{array}{l}{f({x_0})=0}\\{f'({x_0})=0}\end{array}}\right.$,∴$\left\{{\begin{array}{l}{x_0^2+\frac{2}{x_0}-aln{x_0}=0}\\{2x_0^3-a{x_0}-2=0}\end{array}}\right.$消去可得:$2ln{x_0}=1+\frac{3}{x_0^3-1}$,
即$2ln{x_0}-(1+\frac{3}{x_0^3-1})=0$
令$t(x)=2lnx-1-\frac{3}{{{x^3}-1}}(x>1)$,则t(x)在区间(1,+∞)上单调递增
又∵$t(2)=2ln2-1-\frac{3}{{{2^3}-1}}=2×0.6973-1-\frac{3}{7}<2×\frac{7}{10}-1-\frac{3}{7}=-\frac{1}{35}<0$$t(3)=2ln3-1-\frac{3}{{{3^3}-1}}=2×1.099-1-\frac{3}{26}>2×1-1-\frac{3}{26}=\frac{23}{26}>0$
由零点存在性定理知 t(2)<0,t(3)>0
∴2<x0<3∴[x0]=2. …(12分)
点评 本题考查导数的运用:求单调区间和极值,考查函数零点定理的运用,同时考查分类讨论和构造函数法,以及化简整理的运算能力,具有一定的综合性,属于难题.

| A. | $3\sqrt{2}$ | B. | 4 | C. | $\sqrt{34}$ | D. | 5 |
| A. | 8 | B. | -8 | C. | ±8 | D. | $±\frac{9}{8}$ |

| A. | $\frac{5π}{6}$ | B. | $\frac{4π}{3}$ | C. | $\frac{5π}{3}$ | D. | $\frac{2π}{3}$ |
| 分组 | 频数 | 频率 |
| [50,60) | 5 | 0.05 |
| [60,70) | a | 0.20 |
| [70,80) | 35 | b |
| [80,90) | 25 | 0.25 |
| [90,100) | 15 | 0.15 |
| 合计 | 100 | 1.00 |
(Ⅱ)按频率分布表中的成绩分组,采用分层抽样抽取20人参加学校的“我爱国学”宣传活动,求其中优秀生的人数;
(Ⅲ)在第(Ⅱ)问抽取的优秀生中指派2名学生担任负责人,求至少一人的成绩在[90,100]的概率.
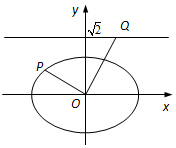 如图,在平面直角坐标系xOy中,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,焦点到相应准线的距离为1.
如图,在平面直角坐标系xOy中,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,焦点到相应准线的距离为1.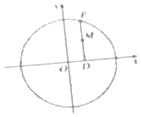 如图,在圆x2+y2=9上任取一点P,过点P作x轴的垂线PD,D为垂足,点M满足$\overrightarrow{DM}=\frac{2}{3}\overrightarrow{DP}$;当点P在圆x2+y2=9上运动时,点M的轨迹为E.
如图,在圆x2+y2=9上任取一点P,过点P作x轴的垂线PD,D为垂足,点M满足$\overrightarrow{DM}=\frac{2}{3}\overrightarrow{DP}$;当点P在圆x2+y2=9上运动时,点M的轨迹为E.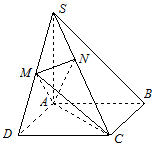 如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB=2,点M是SD的中点,AN⊥SC,且交SC于点N.
如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB=2,点M是SD的中点,AN⊥SC,且交SC于点N.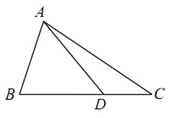 如图,在△ABC中,AB=2,cosB=$\frac{1}{3}$,点D在线段BC上.
如图,在△ABC中,AB=2,cosB=$\frac{1}{3}$,点D在线段BC上.