题目内容
已知圆 的圆心为
的圆心为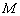 ,
, 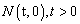 且
且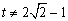 ,设
,设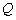 为圆上任一点,线段
为圆上任一点,线段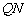 的垂直平分线交直线
的垂直平分线交直线 于点
于点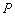 .
.
(1)试讨论动点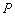 的轨迹类型;
的轨迹类型;
(2)当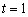 时,设动点
时,设动点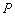 的轨迹为曲线
的轨迹为曲线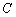 ,过
,过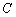 上任一点
上任一点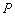 作直线
作直线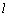 ,
,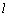 与曲线
与曲线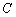 有且只有一个交点,
有且只有一个交点,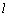 与圆
与圆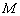 交于点
交于点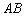 ,若
,若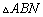 的面积是
的面积是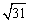 ,求直线
,求直线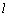 的方程.
的方程.
解:(1)由题
当 时,点
时,点 在圆
在圆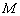 内,点
内,点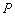 在线段
在线段 内
内
∴
∴动点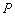 的轨迹是以
的轨迹是以 为焦点,
为焦点, 为长轴的椭圆
为长轴的椭圆
当 时,点
时,点 在圆
在圆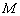 外,点
外,点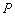 在线段
在线段 的延长线上
的延长线上
∴
∴动点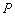 的轨迹是以
的轨迹是以 为焦点,
为焦点, 为实轴长的双曲线
为实轴长的双曲线
(2)由(1)知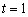 时,动点
时,动点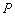 的轨迹是以
的轨迹是以 为焦点,
为焦点, 为长轴长的椭圆
为长轴长的椭圆
∴
∴曲线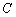 的方程是
的方程是
当直线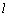 的斜率存在时,设直线
的斜率存在时,设直线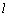 的方程为
的方程为
由 消
消 并整理成
并整理成 (*)
(*)
∵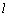 与曲线
与曲线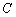 有且只有一个交点
有且只有一个交点
∴(*)方程有且只有一个实数解
∴ 即有
即有
∵圆心 到直线
到直线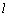 的距离为
的距离为 ,
,
∴弦长
点 到直线
到直线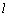 的距离为
的距离为
∴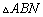 的面积为
的面积为 即
即

∴ =
=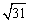 得
得
∴
∴
当 时,代入
时,代入 得
得
当 时,代入
时,代入 得
得
当直线的斜率不存在时,直线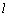 方程为
方程为 或
或 经检验不满足条件
经检验不满足条件
综上所求直线方程为 或
或

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 中,设点
中,设点 是点
是点 关于坐标平面
关于坐标平面 的对称点,则线段
的对称点,则线段
 满足约束条件
满足约束条件 则
则 的最大值为 .
的最大值为 . ,方程
,方程 恰有三个不同的实数根,则实数
恰有三个不同的实数根,则实数 的取值范围是( )
的取值范围是( )
 B.
B.
 D.
D.

 ,下列描述正确的是
,下列描述正确的是 B. 开口向上,焦点为
B. 开口向上,焦点为
 D. 开口向右,焦点为
D. 开口向右,焦点为
 是椭圆
是椭圆 上的一点,
上的一点,  是焦点, 且
是焦点, 且 , 则△
, 则△ 的
的 B.
B. C.
C.  D.
D. 
 中,
中, ,则
,则 等于
等于 为数列
为数列 的前
的前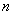 项和,已知
项和,已知 ,若
,若 则
则