题目内容
若实数a，b满足a2+b2-4b+3=0，函数f（x）=asin2x+bcos2x+1的最大值为φ（a，b），则φ（a，b）的最小值为（ ）
| A、2 | ||
B、
| ||
C、
| ||
| D、3 |
考点：两角和与差的正弦函数
专题：计算题,三角函数的求值
分析：先将a2+b2-4b+3=0配方，求出b的取值范围，再求出a2+b2的取值范围，运用两角和的正弦公式，并化简函数f（x）=asin2x+bcos2x+1，求出最大值，再根据a2+b2的范围，求出其最小值．
解答：
解：∵实数a，b满足a2+b2-4b+3=0，
∴a2+（b-2）2=1，∴（b-2）2≤1，解得1≤b≤3，
∴a2+b2=1-（b-2）2+b2=4b-3，
∴1≤4b-3≤9，
∵函数f（x）=asin2x+bcos2x+1
=
sin(2x+θ)+1（θ为辅助角），
∴φ（a，b）=
+1，
∵1≤a2+b2≤9，
∴1≤
≤3，
∴φ（a，b）的最小值为2．
故选：A．
∴a2+（b-2）2=1，∴（b-2）2≤1，解得1≤b≤3，
∴a2+b2=1-（b-2）2+b2=4b-3，
∴1≤4b-3≤9，
∵函数f（x）=asin2x+bcos2x+1
=
| a2+b2 |
∴φ（a，b）=
| a2+b2 |
∵1≤a2+b2≤9，
∴1≤
| a2+b2 |
∴φ（a，b）的最小值为2．
故选：A．
点评：本题考查主要考查两角和的正弦函数公式，考查给定条件下函数的最值问题，注意自变量b的范围确定，本题也是一道易错题．
练习册系列答案
相关题目
对某商店一个月内每天的顾客人数进行了统计，得到样本的茎叶图（如图所示），则该样本的中位数、众数、极差分别是已知a＞0，b＞0，若不等式
+
≥
恒成立，则m的最大值为（ ）
| 3 |
| a |
| 1 |
| b |
| m |
| a+3b |
| A、9 | B、12 | C、18 | D、24 |
“点M（a，b）在函数y=log2x的图象上”是“点N（a4，4b）在函数y=log2x的图象上”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
复数
等于（ ）
| 3-2i |
| 2i |
A、-1+
| ||
B、1-
| ||
C、-1-
| ||
D、1+
|
定义在R上的函数满足f（x+2）=f（x），且x∈[1，3]时，f（x）=cos
x，则下列大小关系正确的是（ ）
| π |
| 2 |
A、f（tan1）＞f（
| ||||
B、f（cos
| ||||
| C、f（sin2）＞f（cos2） | ||||
| D、f（cos1）＞f（sin1） |
已知a=sin
sin
，b=cos2
，c=cos
-sin
，则（ ）
| π |
| 8 |
| 5π |
| 8 |
| π |
| 12 |
| π |
| 12 |
| π |
| 12 |
| A、a＜c＜b |
| B、a＜b＜c |
| C、b＜a＜c |
| D、c＜a＜b |
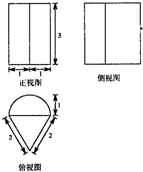
某几何体的三视图如图所示，则该几何体的体积等于（ ）
A、
| ||||
B、3（
| ||||
C、3（
| ||||
D、
|