题目内容
9.|$\overrightarrow{a}$|=4,|$\overrightarrow{b}$|=3,且(3$\overrightarrow{a}$-$\overrightarrow{b}$)⊥($\overrightarrow{a}$-2$\overrightarrow{b}$),求$\overrightarrow{a}$与$\overrightarrow{b}$夹角的余弦值.分析 根据向量的数量积运算和模的运算,以及向量垂直的条件得$\overrightarrow{a}•\overrightarrow{b}$=$\frac{66}{7}$,再根据向量的夹角公式计算即可.
解答 解:∵|$\overrightarrow{a}$|=4,|$\overrightarrow{b}$|=3,
∵(3$\overrightarrow{a}$-$\overrightarrow{b}$)⊥($\overrightarrow{a}$-2$\overrightarrow{b}$),
∴(3$\overrightarrow{a}$-$\overrightarrow{b}$)•($\overrightarrow{a}$-2$\overrightarrow{b}$)=0,
∴3|$\overrightarrow{a}$|2+2|$\overrightarrow{b}$|2-7($\overrightarrow{a}•\overrightarrow{b}$)=0,
∴$\overrightarrow{a}•\overrightarrow{b}$=$\frac{66}{7}$,
设$\overrightarrow{a}$与$\overrightarrow{b}$夹角为θ,
∴cosθ=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$=$\frac{\frac{66}{7}}{4×3}$=$\frac{11}{14}$.
点评 本题考查平面向量的坐标运算和数量积判断两个平面垂直条件的灵活运用,解题时要认真审题,仔细解答.是基础题

练习册系列答案
 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
20. 如图△A′B′C′是△ABC的直观图,其中A′B′=A′C,那么△ABC是( )
如图△A′B′C′是△ABC的直观图,其中A′B′=A′C,那么△ABC是( )
 如图△A′B′C′是△ABC的直观图,其中A′B′=A′C,那么△ABC是( )
如图△A′B′C′是△ABC的直观图,其中A′B′=A′C,那么△ABC是( )| A. | 等腰三角形 | B. | 直角三角形 | C. | 等腰直角三角形 | D. | 钝角三角形 |
19.设x,y满足约束条件$\left\{\begin{array}{l}{3x+2y≤7}\\{4x-y≤a}\end{array}\right.$,且z=ax+y的最大值为4,则a=( )
| A. | 2 | B. | $\frac{2}{3}$ | C. | -2 | D. | -4 |

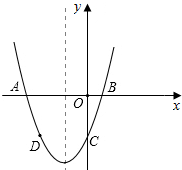 已知二次函数y=x2+bx+c的图象过点A(-3,0)和点B(1,0),且与y轴交于点C,D点在抛物线上且横坐标是-2.
已知二次函数y=x2+bx+c的图象过点A(-3,0)和点B(1,0),且与y轴交于点C,D点在抛物线上且横坐标是-2.