题目内容
已知函数f(x)=log2(x+a).
(Ⅰ)当a=1时,若f(x)+f(x-1)>0成立,求x的取值范围;
(Ⅱ)若定义在R上奇函数g(x)满足g(x+2)=-g(x),且当0≤x≤1时,g(x)=f(x),求g(x)在[-3,-1]上的解析式,并写出g(x)在[-3,3]上的单调区间(不必证明);
(Ⅲ)对于(Ⅱ)中的g(x),若关于x的不等式g(
)≥g(-
)在R上恒成立,求实数t的取值范围.
(Ⅰ)当a=1时,若f(x)+f(x-1)>0成立,求x的取值范围;
(Ⅱ)若定义在R上奇函数g(x)满足g(x+2)=-g(x),且当0≤x≤1时,g(x)=f(x),求g(x)在[-3,-1]上的解析式,并写出g(x)在[-3,3]上的单调区间(不必证明);
(Ⅲ)对于(Ⅱ)中的g(x),若关于x的不等式g(
| t-2x |
| 8+2x+3 |
| 1 |
| 2 |
考点:对数函数图象与性质的综合应用
专题:函数的性质及应用
分析:(Ⅰ)当a=1时,f(x)+f(x-1)>0可化为
,解不等式组可得答案.
(II)根据已知可得a=1,进而根据当x∈[-2,-1]时,x+2∈[0,1],当x∈[-3,-2]时,x+2∈[-1,0],-(x+2)∈[0,1],当0≤x≤1时,g(x)=f(x),可得g(x)在[-3,-1]上的解析式,进而分析出g(x)在[-3,3]上的单调区间;
(III)关于x的不等式g(
)≥g(-
)在R上恒成立,即u=
∈[-
.
],分类讨论后,综合讨论结果,可得答案.
|
(II)根据已知可得a=1,进而根据当x∈[-2,-1]时,x+2∈[0,1],当x∈[-3,-2]时,x+2∈[-1,0],-(x+2)∈[0,1],当0≤x≤1时,g(x)=f(x),可得g(x)在[-3,-1]上的解析式,进而分析出g(x)在[-3,3]上的单调区间;
(III)关于x的不等式g(
| t-2x |
| 8+2x+3 |
| 1 |
| 2 |
| t-2x |
| 8+2x+3 |
| 1 |
| 2 |
| 5 |
| 2 |
解答:
解:(Ⅰ)当a=1时,f(x)=log2(x+1).
∴f(x-1)=log2x,
∴f(x)+f(x-1)=log2(x+1)+log2x=log2[x(x+1)],
若f(x)+f(x-1)>0,则
,
解得:x∈(
,+∞),
即x的取值范围为(
,+∞);
(Ⅱ)∵函数g(x)是定义在R上奇函数,
故g(0)=0,
又∵当0≤x≤1时,g(x)=f(x)=log2(x+a).
故a=1,
当x∈[-2,-1]时,x+2∈[0,1],
∴g(x)=-g(x+2)=-log2(x+3).
当x∈[-3,-2]时,x+2∈[-1,0],-(x+2)∈[0,1],
∴g(x)=-g(x+2)=g[-(x+2)]=log2[-(x+2)+1]=log2(-x-1).
故g(x)=
,
g(x)在[-3,-1]和[1,3]上递减,在[-1,1]上递增;
(III)记u=
=-
+
,
当t+1≥0时,u∈(-
,-
+
)=(-
,
),
由g(
)≥g(-
)在R上恒成立可得:(-
,
)∈[-
.
],
解得:t∈[-1,20].
当t+1<0时,u∈(-
+
,-
)=(
,-
),
由g(
)≥g(-
)在R上恒成立可得:(
,-
)∈[-
.
],
解得:t∈[-4,-1).
综上所述实数t的取值范围为[-4,20].
∴f(x-1)=log2x,
∴f(x)+f(x-1)=log2(x+1)+log2x=log2[x(x+1)],
若f(x)+f(x-1)>0,则
|
解得:x∈(
| ||
| 2 |
即x的取值范围为(
| ||
| 2 |
(Ⅱ)∵函数g(x)是定义在R上奇函数,
故g(0)=0,
又∵当0≤x≤1时,g(x)=f(x)=log2(x+a).
故a=1,
当x∈[-2,-1]时,x+2∈[0,1],
∴g(x)=-g(x+2)=-log2(x+3).
当x∈[-3,-2]时,x+2∈[-1,0],-(x+2)∈[0,1],
∴g(x)=-g(x+2)=g[-(x+2)]=log2[-(x+2)+1]=log2(-x-1).
故g(x)=
|
g(x)在[-3,-1]和[1,3]上递减,在[-1,1]上递增;
(III)记u=
| t-2x |
| 8+2x+3 |
| 1 |
| 8 |
| t+1 |
| 8+2x+3 |
当t+1≥0时,u∈(-
| 1 |
| 8 |
| 1 |
| 8 |
| t+1 |
| 8 |
| 1 |
| 8 |
| t |
| 8 |
由g(
| t-2x |
| 8+2x+3 |
| 1 |
| 2 |
| 1 |
| 8 |
| t |
| 8 |
| 1 |
| 2 |
| 5 |
| 2 |
解得:t∈[-1,20].
当t+1<0时,u∈(-
| 1 |
| 8 |
| t+1 |
| 8 |
| 1 |
| 8 |
| t |
| 8 |
| 1 |
| 8 |
由g(
| t-2x |
| 8+2x+3 |
| 1 |
| 2 |
| t |
| 8 |
| 1 |
| 8 |
| 1 |
| 2 |
| 5 |
| 2 |
解得:t∈[-4,-1).
综上所述实数t的取值范围为[-4,20].
点评:本题考查的知识点是对数函数的图象与性质,对数不等式的解法,求函数的解析式,恒成立问题,是函数图象和性质的综合应用,难度较大,属于难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设直线y=x+b是曲线y=ex的一条切线,则实数b=( )
| A、-1 | B、0 | C、1 | D、2 |
已知函数f(x)在x0处可导,则
等于( )
| lim |
| △x→0 |
| f(x0-2h)-f(x0) |
| h |
| A、2f′(x0) |
| B、-f′(-x0) |
| C、-f′(x0) |
| D、-2f′(x0) |
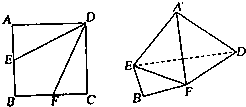 如图,在边长为2的正方形ABCD中,E,F分别是AB,BC的中点,将△ADE,△CDF分别沿DE,DF折起,使A,C两点重合于点A′.
如图,在边长为2的正方形ABCD中,E,F分别是AB,BC的中点,将△ADE,△CDF分别沿DE,DF折起,使A,C两点重合于点A′.