题目内容
20.在平面直角坐标系xOy中,从区域Ω:$\left\{\begin{array}{l}{x-y≤0}\\{x+y-2≤0}\\{x≥0}\end{array}\right.$内随机抽取一点P,则P点到坐标原点的距离大于$\sqrt{2}$的概率为1-$\frac{π}{4}$.分析 作出不等式组对应的平面区域,由几何概型的公式可知概率即为面积之比,易得答案.
解答 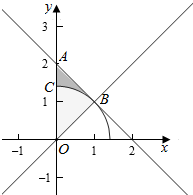 解:作出不等式组对应的平面区域如图,(△AOB内部),
解:作出不等式组对应的平面区域如图,(△AOB内部),
则P点到坐标原点的距离大于$\sqrt{2}$的部分为△AOB内圆外部分,
则B(1,1),△AOB的面积S=$\frac{1}{2}×2×1$=1,
扇形的面积S=$\frac{1}{8}×π×(\sqrt{2})^{2}$=$\frac{π}{4}$,
则△AOB内圆外部分的面积S=1-$\frac{π}{4}$,
则对应的概率P=$\frac{1-\frac{π}{4}}{1}$=1-$\frac{π}{4}$,
故答案为:1-$\frac{π}{4}$.
点评 本题主要考查几何概型的概率的计算,根据条件作出对应的平面区域,求出对应的面积是解决本题的关键.

练习册系列答案
相关题目
11.如图,在四边形ABCD中,设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$,$\overrightarrow{BC}=\overrightarrow c$,则$\overrightarrow{DC}$=( )


| A. | $\overrightarrow a-\overrightarrow b+\overrightarrow c$ | B. | $\overrightarrow b-(\overrightarrow a+\overrightarrow c)$ | C. | $\overrightarrow a+\overrightarrow b+\overrightarrow c$ | D. | $\overrightarrow b-\overrightarrow a+\overrightarrow c$ |
9.已知正数x,y满足x+4y=4,则$\frac{x+28y+4}{xy}$的最小值为( )
| A. | $\frac{85}{2}$ | B. | 24 | C. | 20 | D. | 18 |
10.甲、乙两艘救助船相距1海里,经测量求救呼叫信号发出的位置与这两船构成的角度是救助船甲与救助船乙、求救呼叫信号发出的位置所构成角度的一半,可以判断三者构成的三角形是锐角三角形,则求救呼叫信号发出的位置与救助船乙的距离范围是( )
| A. | (1,2) | B. | (1,$\sqrt{2}$) | C. | (1,$\sqrt{3}$) | D. | ($\sqrt{2}$,$\sqrt{3}$) |