题目内容
9.已知正数x,y满足x+4y=4,则$\frac{x+28y+4}{xy}$的最小值为( )| A. | $\frac{85}{2}$ | B. | 24 | C. | 20 | D. | 18 |
分析 根据已知可将$\frac{x+28y+4}{xy}$,化为$\frac{\frac{{x}^{2}}{2}+2xy+8xy+32{y}^{2}}{xy}$,利用基本不等式可得$\frac{{x}^{2}}{2}+32{y}^{2}$≥2$\sqrt{\frac{{x}^{2}}{2}×32{y}^{2}}$=8xy,从而原式:$\frac{x+28y+4}{xy}$≥$\frac{8xy+2xy+8xy}{xy}$=18.
解答 解:∵x+4y=4,可得:$\frac{x+4y}{4}$=1,
∴$\frac{x+28y+4}{xy}$=$\frac{x+28y+x+4y}{xy}$=$\frac{2x+32y}{xy}$=$\frac{(2x+32y)\frac{x+4y}{4}}{xy}$
=$\frac{\frac{{x}^{2}}{2}+2xy+8xy+32{y}^{2}}{xy}$,
∵$\frac{{x}^{2}}{2}+32{y}^{2}$≥2$\sqrt{\frac{{x}^{2}}{2}×32{y}^{2}}$=8xy,
∴$\frac{x+28y+4}{xy}$≥$\frac{8xy+2xy+8xy}{xy}$=18.
故选:D.
点评 本题主要考查了基本不等式的应用,考查了转化思想和计算能力,属于中档题.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
19.设全集U={1,2,3,4,5},集合M={1,4},N={1,3,5},则N∩(∁UM)等于( )
| A. | {1,3} | B. | {1,5} | C. | {3,5} | D. | {4,5} |
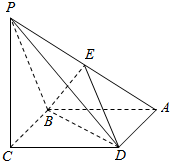 如图所示,已知四棱锥P-ABCD的底面是边长为a的菱形,且∠ABC=120°,PC⊥平面ABCD,PC=a,E为PA的中点.
如图所示,已知四棱锥P-ABCD的底面是边长为a的菱形,且∠ABC=120°,PC⊥平面ABCD,PC=a,E为PA的中点.