题目内容
12.已知函数f(x)的定义域为R,直线x=1和x=2都是曲线y=f(x)的对称轴,且f(0)=1,则f(4)+(10)=2.分析 根据题意和函数对称性的性质求出函数的周期,由周期性可求出f(4)、f(10),代入式子求出答案.
解答 解:因为直线x=1和x=2都是曲线y=f(x)的对称轴,
所以f(2-x)=f(x),f(4-x)=f(x),
则f(2-x)=f(4-x),即f(x+2)=f(x+4),
令x取x-2代入得,f(x)=f(x+2),
所以函数f(x)的最小正周期是2,
又f(0)=1,则f(4)=f(10)=f(0)=1,
所以f(4)+f(10)=2,
故答案为:2.
点评 本题考查函数的对称性、周期性的灵活应用,牢记有关的结论是解题的关键,属于基础题.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
2.如图是一个几何体的三视图,则这个几何体的表面积是( )
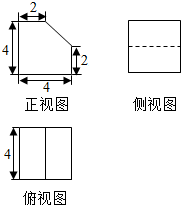

| A. | 84 | B. | $76+8\sqrt{2}$ | C. | $78+8\sqrt{2}$ | D. | $80+8\sqrt{2}$ |
3.在空间在,设m,n,l是三条不同的直线,α,β是两个不同的平面,则下列命题中正确的是( )
| A. | 若m⊥l,n⊥l,则m∥n | B. | 若m∥α,n∥α,则m∥n | C. | 若m⊥α,m⊥β,则α∥β | D. | 若m∥α,m∥β,则α∥β |
1.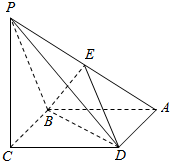 如图所示,已知四棱锥P-ABCD的底面是边长为a的菱形,且∠ABC=120°,PC⊥平面ABCD,PC=a,E为PA的中点.
如图所示,已知四棱锥P-ABCD的底面是边长为a的菱形,且∠ABC=120°,PC⊥平面ABCD,PC=a,E为PA的中点.
(1)求证:平面EBD⊥平面ABCD;
(2)求二面角A-BE-D的大小.
 如图所示,已知四棱锥P-ABCD的底面是边长为a的菱形,且∠ABC=120°,PC⊥平面ABCD,PC=a,E为PA的中点.
如图所示,已知四棱锥P-ABCD的底面是边长为a的菱形,且∠ABC=120°,PC⊥平面ABCD,PC=a,E为PA的中点.(1)求证:平面EBD⊥平面ABCD;
(2)求二面角A-BE-D的大小.
2.两个非零向量$\overrightarrow{AB}$与$\overrightarrow{AC}$满足($\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$+$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$)•$\overrightarrow{BC}$=$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$•$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$=0,则△ABC为( )
| A. | 等边三角形 | B. | 等腰直角三角形 | ||
| C. | 直角非等腰三角形 | D. | 等腰非直角三角形 |