题目内容
10.将正方形ABCD沿对角线BD折成直二面角A-BC-C,有如下四个结论:①AC⊥BD;②△ABC是等边三角形;
③AB与CD所成的角90°;④二面角A-BC-D的平面角正切值是$\sqrt{2}$;
其中正确结论是①②④.(写出所有正确结论的序号)
分析 假设正方形边长为1,作出直观图,根据面面垂直的性质和正方形的性质进行判断.
解答 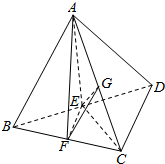 解:取BD中点E,连结AE,CE,则AE⊥BD,CE⊥BD,∴BD⊥平面ACE,∴AC⊥BD.故①正确.
解:取BD中点E,连结AE,CE,则AE⊥BD,CE⊥BD,∴BD⊥平面ACE,∴AC⊥BD.故①正确.
设折叠前正方形的边长为1,则BD=$\sqrt{2}$,∴AE=CE=$\frac{\sqrt{2}}{2}$.
∵平面ABD⊥平面BCD,∴AE⊥平面BCD,∴AE⊥CE,∴AC=$\sqrt{A{E}^{2}+C{E}^{2}}$=1.
∴△ABC是等边三角形,故②正确.
取BC中点F,AC中点G,连结EF,FG,EG,则EF∥CD,FG∥AB,
∴∠EFG为异面直线AB,CD所成的角,在△EFG中,EF=$\frac{1}{2}$CD=$\frac{1}{2}$,FG=$\frac{1}{2}$AB=$\frac{1}{2}$,EG=$\frac{1}{2}$AC=$\frac{1}{2}$,
∴△EFG是等边三角形,∴∠EFG=60°,故③错误.
∵AF⊥BC,BC⊥CD,EF∥CD,∴∠AFE为二面角A-BC-D的平面角.
∵AE⊥EF,∴tan∠AFE=$\frac{AE}{EF}$=$\frac{\frac{\sqrt{2}}{2}}{\frac{1}{2}}$=$\sqrt{2}$.故④正确.
故答案为:①②④.
点评 本题考查了空间线面的位置关系和空间角的求法,属于中档题.

练习册系列答案
相关题目
1.已知y=excosx,则( )
| A. | y′=-exsinx | B. | y′=ex-sinx | C. | y′=$\sqrt{2}$exsin(x+$\frac{π}{4}$) | D. | y′=$\sqrt{2}$exsin($\frac{π}{4}$-x) |
2.如图是一个几何体的三视图,则这个几何体的表面积是( )
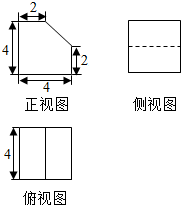

| A. | 84 | B. | $76+8\sqrt{2}$ | C. | $78+8\sqrt{2}$ | D. | $80+8\sqrt{2}$ |
19.设全集U={1,2,3,4,5},集合M={1,4},N={1,3,5},则N∩(∁UM)等于( )
| A. | {1,3} | B. | {1,5} | C. | {3,5} | D. | {4,5} |
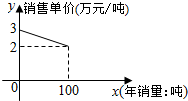 某种产品的成本f1(x)(万元)与年产量x(吨)之间的函数关系是f1(x)=$\frac{1}{100}$x2,该产品的销售单价f2(x)可以表示为关于年销量的一次函数,其部分图象如图所示,且生产的产品都能在当年销售完.
某种产品的成本f1(x)(万元)与年产量x(吨)之间的函数关系是f1(x)=$\frac{1}{100}$x2,该产品的销售单价f2(x)可以表示为关于年销量的一次函数,其部分图象如图所示,且生产的产品都能在当年销售完.