题目内容
8.1101011(2)=412(5).分析 先把二进制数化为十进制数,再把十进制数化为五进制数即可.
解答 解:把二进制数化为十进制数如下,
1101011(2)=1×26+1×25+0×24+1×23+0×22+1×21+1×20=107,
把十进制数化为五进制数如下,
107=4×52+1×51+2×50=412(5).
故答案为:412.
点评 本题考查了二进制数化为五进制数的应用问题,是基础题目.

练习册系列答案
 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 互动课堂系列答案
互动课堂系列答案
相关题目
3.已知某海滨浴场的海浪高度y(米)是时间t(0≤t≤24,单位:小时)的函数,记作:y=f(t),下表是某日各时的浪高数据:
经长期观测,y=f(t)的曲线可近似地看成是函数y=Acosωt+b(A>0,ω>0)
(1)根据以上数据,求出函数y=Acosωt+b的最小正周期T、振幅A及函数表达式
(2)依据规定,当海浪高度高于0.75米时才对冲浪爱好者开放,则一天内的上午8:00至晚上24:00之间,有多少时间可供冲浪爱好者进行运动?
| t(时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y(米) | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 | 1 | 0.5 | 0.99 | 1.5 |
(1)根据以上数据,求出函数y=Acosωt+b的最小正周期T、振幅A及函数表达式
(2)依据规定,当海浪高度高于0.75米时才对冲浪爱好者开放,则一天内的上午8:00至晚上24:00之间,有多少时间可供冲浪爱好者进行运动?
13.2015年9月3号,抗战胜利70周年纪念活动在北京隆重举行,受到全国瞩目,纪念活动包括纪念大会、阅兵式、招待会和文化晚会(招待会和文化晚会算1项活动)等3项,据统计,其中有60名抗战老兵由于身体原因,参加这3项活动的情况如下表所示:
(Ⅰ)若从该60名抗战老兵中按照参加项数分层抽样,抽取6人了解情况.再从抽取的6人中选取2人座谈,求这2人至少1人参加了3项活动的概率;
(Ⅱ)医疗部门决定在(Ⅰ)中抽取到的6名抗战老兵中随机抽取2名进行体检,设参加3项活动的抗战老兵有ξ名接受体检,求ξ的分布列和数学期望.
| 参加纪念活动 项数 | 0 | 1 | 2 | 3 |
| 所占比例 | $\frac{1}{6}$ | $\frac{1}{6}$ | $\frac{1}{3}$ | $\frac{1}{3}$ |
(Ⅱ)医疗部门决定在(Ⅰ)中抽取到的6名抗战老兵中随机抽取2名进行体检,设参加3项活动的抗战老兵有ξ名接受体检,求ξ的分布列和数学期望.
17.坐标平面内到点A(1,0),B(1,2)及到直线x=-1的距离都相等的点的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 无数个 |
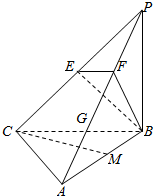 如图,三棱锥P-ABC中,PB⊥底面ABC,∠BCA=90°,PB=BC=CA=4,E为PC的中点,M为AB的中点,点G,F是PA上的三等分点.
如图,三棱锥P-ABC中,PB⊥底面ABC,∠BCA=90°,PB=BC=CA=4,E为PC的中点,M为AB的中点,点G,F是PA上的三等分点.