题目内容
18.已知f(x)=$\frac{sin(kπ-x)}{sinx}$-$\frac{cosx}{cos(kπ-x)}$+$\frac{tan(kπ-x)}{tanx}$-$\frac{cotx}{cot(kπ-x)}$(k∈Z),求f(x)的值域.分析 根据诱导公式,以及分类讨论即可求出函数的值域.
解答 解:当k为偶数时,f(x)=$\frac{sin(kπ-x)}{sinx}$-$\frac{cosx}{cos(kπ-x)}$+$\frac{tan(kπ-x)}{tanx}$-$\frac{cotx}{cot(kπ-x)}$=-$\frac{sinx}{sinx}$-$\frac{cosx}{cosx}$+$\frac{-tanx}{tanx}$-$\frac{costx}{costx}$=1-1-1+1=-2,
当k为奇数时,f(x)=$\frac{sin(kπ-x)}{sinx}$-$\frac{cosx}{cos(kπ-x)}$+$\frac{tan(kπ-x)}{tanx}$-$\frac{cotx}{cot(kπ-x)}$=$\frac{sinx}{sinx}$+$\frac{cosx}{cosx}$+$\frac{-tanx}{tanx}$-$\frac{costx}{costx}$=1+1-1+1=2,
故函数的值域为{-2,2}.
点评 本题主要考查了诱导公式,以及分类讨论的思想,属于基础题.

练习册系列答案
相关题目
3.已知f(x-1)=2x,则f(3)=( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
10.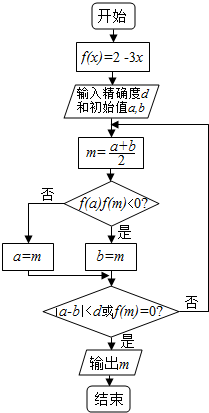 阅读如图所示的程序框图,若输出d=0.1,a=0,b=0.5,则输出的结果是( )
阅读如图所示的程序框图,若输出d=0.1,a=0,b=0.5,则输出的结果是( )
参考数据:
 阅读如图所示的程序框图,若输出d=0.1,a=0,b=0.5,则输出的结果是( )
阅读如图所示的程序框图,若输出d=0.1,a=0,b=0.5,则输出的结果是( )参考数据:
| x | f(x)=2x-3x |
| 0.25 | 0.44 |
| 0.375 | 0.17 |
| 0.4375 | 0.04 |
| 0.46875 | -0.02 |
| 0.5 | -0.08 |
| A. | 0.375 | B. | 0.4375 | C. | 0.46875 | D. | 0.5 |
7.设实数x,y满足$\left\{\begin{array}{l}{2x-y+1≤0}\\{y≤-x-k}\\{x≥0}\end{array}\right.$(k为常数),若目标函数z=3x-y的最大值为-$\frac{1}{3}$,则点(x,y)构成的平面区域Ω的面积为( )
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | 2 | D. | 4 |