题目内容
19.已知命题p:“存在x∈R,x2-2x+m≤0”,命题q:“曲线$\frac{x^2}{5-m}+\frac{y^2}{1+m}=1$表示焦点在x轴上的椭圆”,命题r:t<m<t+1(1)若“p且q”是真命题,求m的取值范围;
(2)若q是r的必要不充分条件,求t的取值范围.
分析 (1)若p为真:△≥0;若q为真:则$\left\{\begin{array}{l}5-m>1+m\\ 1+m>0\end{array}\right.$,若“p且q”是真命题,求其交集即可得出;
(2)由q是r的必要不充分条件,则可得(t,t+1)?(-1,2),解出即可得出.
解答 解:(1)若p为真:△=4-4m≥0--------(1分)
解得m≤1--------(2分)
若q为真:则$\left\{\begin{array}{l}5-m>1+m\\ 1+m>0\end{array}\right.$------(3分)
解得-1<m<2--------(4分)
若“p且q”是真命题,则$\left\{\begin{array}{l}m≤1\\-1<m<2\end{array}\right.$--------(6分)
解得-1<m≤1--------(7分)
(2)由q是r的必要不充分条件,则可得(t,t+1)?(-1,2)-------(11分)
即$\left\{\begin{array}{l}t≥-1\\ t+1≤2\end{array}\right.$(等号不同时成立)-------(13分)
解得-1≤t≤1--------(15分)
点评 本题考查了简易逻辑的判定方法、一元二次不等式的解集与判别式的关系、不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
10.将函数y=(2x-2)ex-1的图象向左平移1个单位得到函数f(x)的图象,则( )
| A. | x=-$\frac{1}{2}$为f(x)的极大值点 | B. | x=1为f(x)的极小值点 | ||
| C. | x=-1为f(x)的极大值点 | D. | x=-1为f(x)的极小值点 |
7.在如图所示的程序框图中,若a=($\frac{1}{16}$)${\;}^{\frac{1}{2}}$,b=log42,c=log23•log32,则输出的x等于( )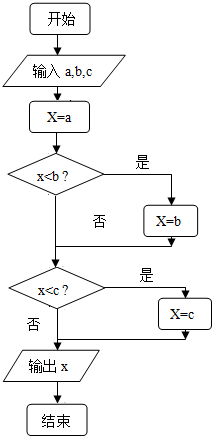

| A. | 0.25 | B. | 0.5 | C. | 1 | D. | 2 |
14.已知一个算法的程序框图如图所示,当输出的结果为0时,输入的x的值为( )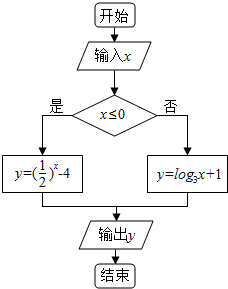

| A. | -2 | B. | -2或-1 | C. | 1或-3 | D. | -2或$\frac{1}{3}$ |
4.执行如图所示的程序框图.当输入-2时,输出的y值为( )


| A. | -2 | B. | 0 | C. | 2 | D. | ±2 |
