题目内容
20.已知P为圆C:x2+y2=2上一点,过点P作y轴的垂线交y轴于点Q,点M满足$\overrightarrow{QM}$=2$\overrightarrow{QP}$.(1)求动点M的轨迹方程;
(2)设N为直线l:x=4上一点,O为坐标原点,且OM⊥ON,求△MON面积的最小值.
分析 (1)设出M点的坐标,由题意可得P为线段QM的中点,由中点坐标公式得到P的坐标,把P的坐标代入圆x2+y2=2整理得动点M的轨迹方程;
(2)求出当OM斜率不存在时的△MON面积为$2\sqrt{2}$,再由OM斜率存在不为0时△MON面积大于$2\sqrt{2}$得答案.
解答 解:(1)设M(x,y),由题意Q(0,y),P(x1,y),
由$\overrightarrow{QM}$=2$\overrightarrow{QP}$,知P为QM的中点,
∴x+0=2x1,x1=$\frac{x}{2}$,
又∵P(x1,y)在圆x2+y2=2上,
∴$\frac{{x}^{2}}{4}+{y}^{2}=2$,
即$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{2}=1$,
∴动点M的轨迹方程为$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{2}=1$;
(2)由题意可知,①当OM斜率不存在时,|OM|=$\sqrt{2}$,|ON|=4,
此时△MON面积等于$\frac{1}{2}×4×\sqrt{2}=2\sqrt{2}$;
②当OM斜率为0时,△MON不存在;
③当OM斜率存在不为0时,设OM所在直线方程为y=kx,则ON所在直线方程为y=-$\frac{1}{k}x$,
联立$\left\{\begin{array}{l}{y=kx}\\{\frac{{x}^{2}}{8}+\frac{{y}^{2}}{2}=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{{x}^{2}=\frac{8}{1+4{k}^{2}}}\\{{y}^{2}=\frac{8{k}^{2}}{1+4{k}^{2}}}\end{array}\right.$,
联立$\left\{\begin{array}{l}{y=-\frac{1}{k}x}\\{x=4}\end{array}\right.$,解得N(4,$-\frac{4}{k}$),
∴|OM|=$\sqrt{{x}^{2}+{y}^{2}}=\sqrt{\frac{8(1+{k}^{2})}{1+4{k}^{2}}}$=$\sqrt{2}\sqrt{\frac{4+4{k}^{2}}{1+4{k}^{2}}}>\sqrt{2}$,|ON|=$\sqrt{16+\frac{16}{{k}^{2}}}=4\sqrt{\frac{1+{k}^{2}}{{k}^{2}}}$>4.
∴${S}_{△OMN}=\frac{1}{2}|OM||ON|>\frac{1}{2}×\sqrt{2}×4=2\sqrt{2}$.
综合①②③,△MON面积的最小值为$2\sqrt{2}$.
点评 本题考查点的轨迹方程的求法,考查直线与圆锥曲线的位置关系,考查运算能力,属于中档题.

| A. | x=-$\frac{1}{2}$为f(x)的极大值点 | B. | x=1为f(x)的极小值点 | ||
| C. | x=-1为f(x)的极大值点 | D. | x=-1为f(x)的极小值点 |
| A. | $\frac{13}{15}$ | B. | $\frac{13}{18}$ | C. | $\frac{15}{16}$ | D. | $\frac{13}{16}$ |
| A. | 若命题“p∧q”为真命题,则“p∨q”为真命题 | |
| B. | 命题“若m>0,则方程x2+x-m=0有实根”的逆命题为真命题 | |
| C. | 命题“若a>b,则ac2>bc2”的否命题为真命题 | |
| D. | 若命题“¬p∨q”为假命题,则“p∧¬q”为真命题 |
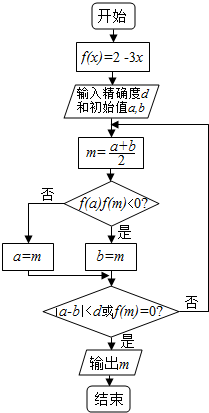 阅读如图所示的程序框图,若输出d=0.1,a=0,b=0.5,则输出的结果是( )
阅读如图所示的程序框图,若输出d=0.1,a=0,b=0.5,则输出的结果是( )参考数据:
| x | f(x)=2x-3x |
| 0.25 | 0.44 |
| 0.375 | 0.17 |
| 0.4375 | 0.04 |
| 0.46875 | -0.02 |
| 0.5 | -0.08 |
| A. | 0.375 | B. | 0.4375 | C. | 0.46875 | D. | 0.5 |
