题目内容
12.若函数f(x)=$\left\{\begin{array}{l}{(x-a)^{2}}&{(x≤0)}\\{x+\frac{1}{x}+a}&{(x>0)}\end{array}\right.$的最小值为f(0),则实数a的取值范围( )| A. | [-1,2] | B. | [-1,0] | C. | [1,2] | D. | [0,2] |
分析 由分段函数分别讨论函数在不同区间上的最值,从而可得2+a≥a2,又a≥0,从而解得a的范围.
解答 解:当x>0时,f(x)=x+$\frac{1}{x}$+a≥2+a;
(当且仅当x=$\frac{1}{x}$,即x=1时,等号成立);
故当x=1时取得最小值2+a,
∵f(0)是函数f(x)的最小值,
∴当x≤0时,f(x)=(x-a)2单调递减,
故a≥0,
此时的最小值为f(0)=a2,
故2+a≥a2,
解得,-21≤a≤2.
又a≥0,可得0≤a≤2.
故选:D.
点评 本题考查了分段函数的应用及分段函数的最值的求法,注意运用基本不等式和二次函数的单调性,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.已知圆的方程为(x-2)2+(y+3)2=9,则其圆心坐标和半径分别为( )
| A. | (2,-3),3 | B. | (-2,3),3 | C. | (3,-2),3 | D. | (-3,2),3 |
2.经过原点和点(0,-6),且圆心在y轴上的圆的标准方程是( )
| A. | x2+(y+6)2=36 | B. | x2+(y+3)2=36 | C. | x2+(y+3)2=9 | D. | x2+y2=9 |
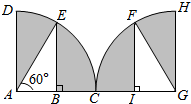 如图所示,两个四分之一圆面ACD和GCH交于点C点,AD=CH=10厘米,∠EAB=∠FGC=60°,EB与FI分别垂直于AC和GC,则阴影部分为85.28平方厘米.(π取3.14)
如图所示,两个四分之一圆面ACD和GCH交于点C点,AD=CH=10厘米,∠EAB=∠FGC=60°,EB与FI分别垂直于AC和GC,则阴影部分为85.28平方厘米.(π取3.14)