题目内容
设函数f（x）=
，又记f1（x）=f（x），fk+1（x）=f（fk（x）），k∈N*），则f2013（2014）= ．
| 1+x |
| 1-x |
考点：数列的函数特性,函数的值
专题：函数的性质及应用
分析：利用函数f（x）=
，又记f1（x）=f（x），fk+1（x）=f（fk（x）），k∈N*），可得fn+4（2014）=fn（2014）．即可得出．
| 1+x |
| 1-x |
解答：
解：∵f1（2014）=f（2014）=
=-
，
∴f2（2014）=f(-
)=
=-
，
∴f3（2014）=f(-
)=
=
．
∴f4（2014）=f(
)=
=2014．
∴f5（2014）=f（2014）=f1（2014）．
…，
∴fn+4（2014）=fn（2014）．
∴f2013（2014）=f1(2014)=-
．
故答案为：-
．
| 1+2014 |
| 1-2014 |
| 2015 |
| 2013 |
∴f2（2014）=f(-
| 2015 |
| 2013 |
1-
| ||
1+
|
| 1 |
| 2014 |
∴f3（2014）=f(-
| 1 |
| 2014 |
1-
| ||
1+
|
| 2013 |
| 2015 |
∴f4（2014）=f(
| 2013 |
| 2015 |
1+
| ||
1-
|
∴f5（2014）=f（2014）=f1（2014）．
…，
∴fn+4（2014）=fn（2014）．
∴f2013（2014）=f1(2014)=-
| 2015 |
| 2013 |
故答案为：-
| 2015 |
| 2013 |
点评：本题考查了数列的周期性、函数的性质，属于中档题．
练习册系列答案
小天才课时作业系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
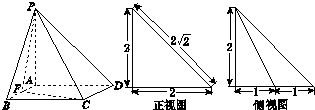如图所示，在四棱锥P-ABCD中，PA⊥底面ABCD，四边形ABCD为正方形，F为AB上一点．该四棱锥的正视图和侧视图如图所示，则四面体P-BFC的体积是在△ABC中，A：B：C=4：1：1，则a：b：c=（ ）
A、
| ||
| B、2：1：1 | ||
C、
| ||
| D、3：1：1 |