题目内容

1．已知直线3x+4y-5=0与直线6x+my+14=0平行，则它们之间的距离是$\frac{12}{5}$．

分析 求出m，转化为直线3x+4y-5=0与直线3x+4y+7=0之间的距离．

解答 解：由题意，m=8，
直线3x+4y-5=0与直线3x+4y+7=0之间的距离是$\frac{|-5-7|}{\sqrt{9+16}}$=$\frac{12}{5}$，
故答案为：$\frac{12}{5}$．

点评 本题考查两条平行线间的距离，考查学生的计算能力，属于中档题．

练习册系列答案
相关题目
11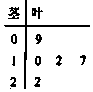．如图是一名篮球运动员在五场比赛中所得分数的茎叶图，则该运动员在这五场比赛中得分的平均数、中位数分别为（　　）
A．14，12B．12，14C．14，10D．10，12
12．已知x＞0，若（x-i）2是纯虚数（其中i为虚数单位），则x=1．
9．已知矩阵$A=[{\begin{array}{l}2&1\\ 3&2\end{array}}]$，列向量$X=[{\begin{array}{l}x\\ y\end{array}}]，B=[{\begin{array}{l}4\\ 7\end{array}}]$，若AX=B，直接写出A-1，并求出X．
16．母线长为1的圆锥的侧面展开图的圆心角等于120°，则该圆锥的体积为（　　）
A．$\frac{{2\sqrt{2}}}{81}π$B．$\frac{{4\sqrt{5}}}{81}π$C．$\frac{8}{81}π$D．$\frac{10}{81}π$
6．如图，四棱锥P-ABCD中，BC∥AD，BC=1，AD=2，AC⊥CD，且平面PCD⊥平面ABCD．
（1）求证：AC⊥PD；
（2）在线段PA上是否存在点E，使BE∥平面PCD？若存在，确定点E的位置，若不存在，请说明理由．
13．某校为了解高二的1553名同学对教师的教学意见，现决定用系统抽样的方法抽取一个容量为50的样本，先在总体中随机剔除n个个体，然后把剩下的个体按0001，0002，0003…编号并分成m个组，则n和m应分别是（　　）
A．53，50B．53，30C．3，50D．3，31
10．已知点P（x0，y0）为椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$上一点，F1，F2分别为椭圆C的左右焦点，当y0=$\frac{b}{2}$时，∠F1PF2=60°，则椭圆C的离心率为（　　）
A．$\frac{{2\sqrt{7}}}{7}$B．$\frac{{\sqrt{7}}}{7}$C．$\frac{1}{2}$D．$\frac{{\sqrt{2}}}{2}$
15．在极坐标系中，求直线$θ=\frac{π}{4}（ρ∈R）$被曲线ρ=4sinθ所截得的弦长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网