题目内容
6. 如图,四棱锥P-ABCD中,BC∥AD,BC=1,AD=2,AC⊥CD,且平面PCD⊥平面ABCD.
如图,四棱锥P-ABCD中,BC∥AD,BC=1,AD=2,AC⊥CD,且平面PCD⊥平面ABCD.(1)求证:AC⊥PD;
(2)在线段PA上是否存在点E,使BE∥平面PCD?若存在,确定点E的位置,若不存在,请说明理由.
分析 (1)利用面面垂直的性质定理证明AC⊥平面PCD,即可证明AC⊥PD;
(2)当点E是线段PA的中点时,BE∥平面PCD.利用已知条件,得到四边形BCFE为平行四边形,再利用线面平行的判定定理即可证明.
解答 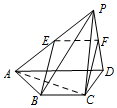 证明:(1)连接AC,
证明:(1)连接AC,
∵平面PCD⊥平面ABCD,平面PCD∩平面ABCD=CD,AC⊥CD,AC?平面ABCD,
∴AC⊥平面PCD,…(4分)
∵PD?平面PCD,所以AC⊥PD.…(5分)
(2)当点E是线段PA的中点时,BE∥平面PCD.…(6分)
证明如下:分别取AP,PD的中点E,F,连接BE,EF,CF.则EF为△PAD的中位线,
所以EF∥AD,且$EF=\frac{1}{2}AD=1$,
又BC∥AD,所以BC∥EF,且BC=EF,
所以四边形BCFE是平行四边形,所以BE∥CF,…(10分)
又因为BE?平面PCD,CF?平面PCD
所以BE∥平面PCD.…(12分)
点评 熟练掌握面面垂直的性质定理、平行线分线段成比例定理在三角形中的应用、平行四边形的判定和性质定理、线面平行的判定定理是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.若直线l1:(k-3)x+(k+4)y+1=0与l2:(k+1)x+2(k-3)y+3=0垂直,则实数k的值是( )
| A. | 3或-3 | B. | 3或4 | C. | -3或-1 | D. | -1或4 |
11.如图,网格纸上小正方形边长为1,粗实线画出的是一个几何体的三视图,则该几何体体积为( )


| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{4π}{3}$ | D. | $\frac{16π}{3}$ |
20.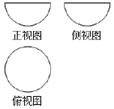 如图是某几何体的三视图,其正视图,侧视图均为直径为2的半圆,俯视图是直径为2的圆,则该几何体的表面积为( )
如图是某几何体的三视图,其正视图,侧视图均为直径为2的半圆,俯视图是直径为2的圆,则该几何体的表面积为( )
 如图是某几何体的三视图,其正视图,侧视图均为直径为2的半圆,俯视图是直径为2的圆,则该几何体的表面积为( )
如图是某几何体的三视图,其正视图,侧视图均为直径为2的半圆,俯视图是直径为2的圆,则该几何体的表面积为( )| A. | 3π | B. | 4π | C. | 5π | D. | 12π |
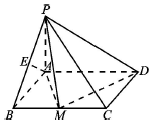 如图,四棱锥P-ABCD,底面ABCD为矩形,AB=PA=$\sqrt{3}$,AD=2,PB=$\sqrt{6}$,E为PB中点,且AE⊥PC.
如图,四棱锥P-ABCD,底面ABCD为矩形,AB=PA=$\sqrt{3}$,AD=2,PB=$\sqrt{6}$,E为PB中点,且AE⊥PC.