题目内容
15.在极坐标系中,求直线$θ=\frac{π}{4}(ρ∈R)$被曲线ρ=4sinθ所截得的弦长.分析 极坐标方程化为直角坐标方程,联立,求出A,B的坐标,即可求直线$θ=\frac{π}{4}(ρ∈R)$被曲线ρ=4sinθ所截得的弦长.
解答 解:以极点O为坐标原点,极轴为x轴的正半轴建立平面直角坐标系.
直线$θ=\frac{π}{4}(ρ∈R)$的直角坐标方程为y=x①,…3分
曲线ρ=4sinθ的直角坐标方程为x2+y2-4y=0②. …6分
由①②得$\left\{\begin{array}{l}x=0\\ y=0\end{array}\right.$或$\left\{\begin{array}{l}x=2\\ y=2\end{array}\right.$…8分
所以A(0,0),B(2,2),
所以直线$θ=\frac{π}{4}(ρ∈R)$被曲线ρ=4sinθ所截得的弦长AB=$2\sqrt{2}$. …10分.
点评 本题考查极坐标方程化为直角坐标方程,考查方程思想,比较基础.

练习册系列答案
相关题目
20.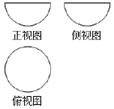 如图是某几何体的三视图,其正视图,侧视图均为直径为2的半圆,俯视图是直径为2的圆,则该几何体的表面积为( )
如图是某几何体的三视图,其正视图,侧视图均为直径为2的半圆,俯视图是直径为2的圆,则该几何体的表面积为( )
 如图是某几何体的三视图,其正视图,侧视图均为直径为2的半圆,俯视图是直径为2的圆,则该几何体的表面积为( )
如图是某几何体的三视图,其正视图,侧视图均为直径为2的半圆,俯视图是直径为2的圆,则该几何体的表面积为( )| A. | 3π | B. | 4π | C. | 5π | D. | 12π |
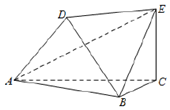 如图,以A、B、C、D、E为顶点的六面体中,△ABC和△ABD均为等边三角形,且平面ABC⊥平面ABD,EC⊥平面ABC,EC=$\sqrt{3}$,AB=2.
如图,以A、B、C、D、E为顶点的六面体中,△ABC和△ABD均为等边三角形,且平面ABC⊥平面ABD,EC⊥平面ABC,EC=$\sqrt{3}$,AB=2.