题目内容
10.已知点P(x0,y0)为椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$上一点,F1,F2分别为椭圆C的左右焦点,当y0=$\frac{b}{2}$时,∠F1PF2=60°,则椭圆C的离心率为( )| A. | $\frac{{2\sqrt{7}}}{7}$ | B. | $\frac{{\sqrt{7}}}{7}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
分析 由P在椭圆上求出P的横坐标,利用焦半径公式及余弦定理得到关于a,c的方程,求解可得椭圆的离心率.
解答 解:由P(x0,y0)在椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$上,且y0=$\frac{b}{2}$,可得${{x}_{0}}^{2}=\frac{3}{4}{a}^{2}$,
不妨取${x}_{0}=\frac{\sqrt{3}}{2}a$,
则$|P{F}_{1}|=a+e{x}_{0}=a+\frac{\sqrt{3}}{2}c$,$|P{F}_{2}|=a-e{x}_{0}=a-\frac{\sqrt{3}}{2}c$.
在△F1PF2中,则$4{c}^{2}=(a+\frac{\sqrt{3}}{2}c)^{2}+(a-\frac{\sqrt{3}}{2}c)^{2}-2({a}^{2}-\frac{3}{4}{c}^{2})•cos60°$,
即$4{c}^{2}={a}^{2}+\sqrt{3}ac+\frac{3}{4}{c}^{2}+{a}^{2}-\sqrt{3}ac+\frac{3}{4}{c}^{2}$$-{a}^{2}+\frac{3}{4}{c}^{2}$.
∴$\frac{{c}^{2}}{{a}^{2}}=\frac{4}{7}$,则$e=\frac{c}{a}=\frac{2\sqrt{7}}{7}$.
故选:A.
点评 本题考查椭圆的简单性质,考查了椭圆焦半径公式的应用,考查利用余弦定理求解焦点三角形问题,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.已知全集U={0,1,3,4,5,6,8},集合A={1,4,5,8},B={2,6},则集合(∁UA)∪B=( )
| A. | {1,2,5,8} | B. | {0,3,6} | C. | {0,2,3,6} | D. | ∅ |
5.书架上有2本不同的语文书,3本不同的数学书,从中任意取出2本,取出的书恰好都是数学书的概率为( )
| A. | $\frac{3}{10}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{7}$ | D. | $\frac{1}{3}$ |
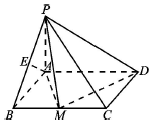 如图,四棱锥P-ABCD,底面ABCD为矩形,AB=PA=$\sqrt{3}$,AD=2,PB=$\sqrt{6}$,E为PB中点,且AE⊥PC.
如图,四棱锥P-ABCD,底面ABCD为矩形,AB=PA=$\sqrt{3}$,AD=2,PB=$\sqrt{6}$,E为PB中点,且AE⊥PC.