题目内容
4.设集合M={x|x2≥x},N={x|log${\;}_{\frac{1}{2}}$(x+1)>0},则有( )| A. | N⊆M | B. | M⊆∁RN | C. | M∩N=∅ | D. | M∪N=R |
分析 化解集合M和N,根据集合的基本运算依次判断即可.
解答 解:集合M={x|x2≥x}={x|x≥1或x≤0},N={x|log${\;}_{\frac{1}{2}}$(x+1)>0}={x|-1<x<0}.
∴N⊆M,故A正确.
故选A.
点评 本题主要考查集合的基本运算,比较基础.

练习册系列答案
相关题目
15.下列函数既是奇函数又在定义域上单调递增的是( )
| A. | $f(x)=\frac{{{x^2}-2x}}{x-2}$ | B. | f(x)=x-$\frac{1}{x}$ | C. | f(x)=2x-2-x | D. | f(x)=x|sinx| |
16. 如图,阴影部分的面积为( )
如图,阴影部分的面积为( )
 如图,阴影部分的面积为( )
如图,阴影部分的面积为( )| A. | 9 | B. | $\frac{9}{2}$ | C. | $\frac{13}{6}$ | D. | $\frac{7}{3}$ |
13.数列{an}满足an+1=$\left\{\begin{array}{l}{2{a}_{n},0≤{a}_{n}≤\frac{1}{2}}\\{2{a}_{n}-1,\frac{1}{2}<{a}_{n}≤1}\end{array}\right.$,若a1=$\frac{3}{5}$,则a2015=( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
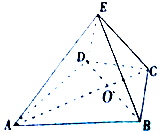 如图,在四棱锥E-ABCD中,△ABD是正三角形,△BCD是等腰三角形,∠BCD=120°,EC⊥BD.
如图,在四棱锥E-ABCD中,△ABD是正三角形,△BCD是等腰三角形,∠BCD=120°,EC⊥BD.