题目内容
设函数f(x)=x2+ax-lnx(a∈R).
(Ⅰ)若a=1,求函数f(x)的单调区间;
(Ⅱ)若函数f(x)在区间(0,1]上是减函数,求实数a的取值范围;
(Ⅲ)过坐标原点O作曲线y=f(x)的切线,证明:切线有且仅有一条,且切点的横坐标恒为1.
(Ⅰ)若a=1,求函数f(x)的单调区间;
(Ⅱ)若函数f(x)在区间(0,1]上是减函数,求实数a的取值范围;
(Ⅲ)过坐标原点O作曲线y=f(x)的切线,证明:切线有且仅有一条,且切点的横坐标恒为1.
考点:利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:导数的概念及应用,导数的综合应用
分析:(Ⅰ)a=1时,f(x)=x2+ax-lnx(x>0),f′(x)=2x+1-
=
,根据函数的定义域,确定f′(x)>0和f′(x)>0的范围,进而得到函数f(x)的单调区间;
(Ⅱ)若函数f(x)在区间(0,1]上是减函数,则f'(x)≤0对任意x∈(0,1]恒成立,进而a≤
-2x对任意x∈(0,1]恒成立,进而将问题转化为函数的最值问题后,可得实数a的取值范围;
(Ⅲ)设出切点坐标,利用导数法求出切线斜率(切点处的导函数值),进而利用点斜式方程结合切线过原点求出切线方程,通过证明t=1是方程t2+lnt-1=0的唯一的解,可得结论.
| 1 |
| x |
| (2x-1)(x+1) |
| x |
(Ⅱ)若函数f(x)在区间(0,1]上是减函数,则f'(x)≤0对任意x∈(0,1]恒成立,进而a≤
| 1 |
| x |
(Ⅲ)设出切点坐标,利用导数法求出切线斜率(切点处的导函数值),进而利用点斜式方程结合切线过原点求出切线方程,通过证明t=1是方程t2+lnt-1=0的唯一的解,可得结论.
解答:
解:(Ⅰ)a=1时,f(x)=x2+ax-lnx(x>0),
∴f′(x)=2x+1-
=
,
又∵x∈(0 ,
) , f′(x)<0 , x∈(
, +∞) , f′(x)>0,
f(x)的单调递减区间为(0 ,
),单调递增区间为(
, +∞).
(Ⅱ)∵f′(x)=2x+a-
又∵f(x)在区间(0,1]上是减函数,
∴f′(x)≤0对任意x∈(0,1]恒成立,
即2x+a-
≤0对任意x∈(0,1]恒成立,
∴a≤
-2x对任意x∈(0,1]恒成立,
令g(x)=
-2x,
∴a≤g(x)min,
易知g(x)在(0,1]单调递减,
∴g(x)min=g(1)=-1.
∴a≤-1.
(Ⅲ)设切点为M(t,f(t)),f′(x)=2x+a-
,
∴过M点的切线方程为:y-f(t)=f′(t)(x-t),
即 y-(t2+at-lnt)=(2t+a-
)(x-t)
又切线过原点,所以,0-(t2+at-lnt)=(2t+a-
)(0-t),
即t2+lnt-1=0,
显然t=1是方程t2+lnt-1=0的解,
设φ(t)=t2+lnt-1,
则φ′(t)=2t+
>0恒成立,φ(t)在(0,+∞)单调递增,且φ(1)=0,
∴方程t2+lnt-1=0有唯一解1.
∴过坐标原点O作曲线y=f(x)的切线,切线有且仅有一条,且切点的横坐标恒为1.
∴f′(x)=2x+1-
| 1 |
| x |
| (2x-1)(x+1) |
| x |
又∵x∈(0 ,
| 1 |
| 2 |
| 1 |
| 2 |
f(x)的单调递减区间为(0 ,
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅱ)∵f′(x)=2x+a-
| 1 |
| x |
又∵f(x)在区间(0,1]上是减函数,
∴f′(x)≤0对任意x∈(0,1]恒成立,
即2x+a-
| 1 |
| x |
∴a≤
| 1 |
| x |
令g(x)=
| 1 |
| x |
∴a≤g(x)min,
易知g(x)在(0,1]单调递减,
∴g(x)min=g(1)=-1.
∴a≤-1.
(Ⅲ)设切点为M(t,f(t)),f′(x)=2x+a-
| 1 |
| x |
∴过M点的切线方程为:y-f(t)=f′(t)(x-t),
即 y-(t2+at-lnt)=(2t+a-
| 1 |
| t |
又切线过原点,所以,0-(t2+at-lnt)=(2t+a-
| 1 |
| t |
即t2+lnt-1=0,
显然t=1是方程t2+lnt-1=0的解,
设φ(t)=t2+lnt-1,
则φ′(t)=2t+
| 1 |
| t |
∴方程t2+lnt-1=0有唯一解1.
∴过坐标原点O作曲线y=f(x)的切线,切线有且仅有一条,且切点的横坐标恒为1.
点评:本题考查的知识点是利用导数研究函数的单调性,利用导数研究曲线上某点的切线方程,是导数的综合应用,难度中档.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知四个数2,a,b,5成等比数列,则等lgab于( )
| A、-1 | B、0 | C、1 | D、2 |
已知向量
=(0,1),
=(1,0),
=(3,4),若λ为实数,且(
+λ
)⊥
,则λ的值为( )
| a |
| b |
| c |
| b |
| a |
| c |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
抛掷3个骰子,当至少一个5点或一个6点出现时,就说这次试验成功,则在54次试验中成功次数n的期望为( )
| A、19 | B、27 | C、54 | D、38 |
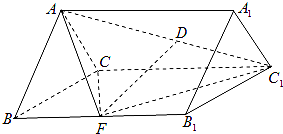 如图,正三棱柱ABC-A1B1C1的各棱长都等于2,D在AC1上,F为BB1中点,且FD⊥AC1.
如图,正三棱柱ABC-A1B1C1的各棱长都等于2,D在AC1上,F为BB1中点,且FD⊥AC1. 如图,已知AB⊥平面α于B,DC?α,且CD⊥AC于C,求证:平面ACD⊥平面ABC.
如图,已知AB⊥平面α于B,DC?α,且CD⊥AC于C,求证:平面ACD⊥平面ABC.