题目内容
若函数f（x）（x∈R）是奇函数，函数g（x）（x∈R）是偶函数，则一定成立的是（ ）
| A、函数f[g（x）]是奇函数 |
| B、函数g[f（x）]是奇函数 |
| C、函数f[f（x）]是奇函数 |
| D、函数g[g（x）]是奇函数 |
考点：函数奇偶性的判断
专题：函数的性质及应用
分析：根据函数奇偶性的定义分别进行判断即可．
解答：
解：∵函数f（x）（x∈R）是奇函数，函数g（x）（x∈R）是偶函数，
则A．f[g（-x）]=f[g（x）]为偶函数．
B．g[f（-x）]=g[-f（x）]=g[f（x）]为偶函数．
C．f[f（-x）]=f[-f（x）]=-f[f（x）]为奇函数．
D．g[g（-x）]=g[g（x）]是偶函数．
故选：C
则A．f[g（-x）]=f[g（x）]为偶函数．
B．g[f（-x）]=g[-f（x）]=g[f（x）]为偶函数．
C．f[f（-x）]=f[-f（x）]=-f[f（x）]为奇函数．
D．g[g（-x）]=g[g（x）]是偶函数．
故选：C
点评：本题主要考查函数奇偶性的判断，利用奇偶性的定义直接代入进行验证即可，比较基础．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
下列各组向量中，可以作为基底的是（ ）
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
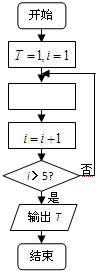如图所示的程序框图，若执行的运算是1×| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| A、T=T•i | ||
| B、T=T•（i+1） | ||
C、T=T•
| ||
D、T=T•
|
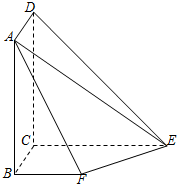如图所示，平面ABCD⊥平面BCEF，且四边形ABCD为矩形，四边形BCEF为直角梯形，BF∥CE，BC⊥CE，DC=CE=4，BC=BF=2．