题目内容
8.设向量$\overrightarrow{AB}$=(2sinx,-1),$\overrightarrow{CD}$=(3,4),x∈(0,π),当|$\overrightarrow{AB}$|取最大值时,向量$\overrightarrow{AB}$在$\overrightarrow{CD}$方向上的投影为( )| A. | $\frac{2}{5}$ | B. | $\frac{2}{5}$或-2 | C. | $\frac{3}{5}$ | D. | $\frac{3}{5}$或-2 |
分析 由向量$\overrightarrow{AB}$的坐标求出模,结合三角函数的有界性求出|$\overrightarrow{AB}$|取最大值时的$\overrightarrow{AB}$的具体坐标,代入投影公式得答案.
解答 解:∵$\overrightarrow{AB}$=(2sinx,-1),
∴$|\overrightarrow{AB}|=\sqrt{(2sinx)^{2}+(-1)^{2}}≤\sqrt{{2}^{2}+1}=\sqrt{5}$x∈(0,π),
∴当2sinx=2时,|$\overrightarrow{AB}$|取最大值,
此时向量$\overrightarrow{AB}$在$\overrightarrow{CD}$方向上的投影为$\frac{\overrightarrow{AB}•\overrightarrow{CD}}{|\overrightarrow{CD}|}=\frac{2×3-4}{5}=\frac{2}{5}$.
故选:A.
点评 本题考查平面向量的数量积运算,考查了向量在向量方向上的投影,是中档题.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
13.下列判断错误的是( )
| A. | “am2<bm2”是“a<b”的充分不必要条件 | |
| B. | 命题“x∈R,x3-x2-1≤0”的否定是“?x0∈R,x${\;}_{0}^{3}$-x${\;}_{0}^{2}$-1>0” | |
| C. | 若p,q均为假命题,则p∧q为假命题 | |
| D. | 函数y=1是幂函数 |
20.函数f(x)=2x-x2的零点所在的一个区间是( )
| A. | (-$\frac{1}{2}$,0) | B. | ($\frac{3}{2}$,$\frac{5}{2}$) | C. | ($\frac{9}{2}$,$\frac{11}{2}$) | D. | (4,+∞) |
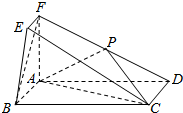 在如图所示的几何体中,四边形ABCD为矩形,平面ABEF⊥平面ABCD,EF∥AB,∠BAF=90°,AD=2,AB=AF=2FE=1,点P是棱DF的中点.
在如图所示的几何体中,四边形ABCD为矩形,平面ABEF⊥平面ABCD,EF∥AB,∠BAF=90°,AD=2,AB=AF=2FE=1,点P是棱DF的中点.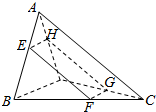 空间四边形ABCD的两条对棱AC,BD互相垂直,AC,BD的长分别为8和2,则平行四边形两条对棱的截面四边形EFGH在平移过程中,面积的最大值是4.
空间四边形ABCD的两条对棱AC,BD互相垂直,AC,BD的长分别为8和2,则平行四边形两条对棱的截面四边形EFGH在平移过程中,面积的最大值是4.