题目内容
20.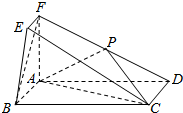 在如图所示的几何体中,四边形ABCD为矩形,平面ABEF⊥平面ABCD,EF∥AB,∠BAF=90°,AD=2,AB=AF=2FE=1,点P是棱DF的中点.
在如图所示的几何体中,四边形ABCD为矩形,平面ABEF⊥平面ABCD,EF∥AB,∠BAF=90°,AD=2,AB=AF=2FE=1,点P是棱DF的中点.(1)求证:AD⊥BF;
(2)求点B到面PCD的距离.
分析 (1)由已知推导出AD⊥AB,利用面面垂直性质定理能证明AD⊥BF.
(2)取AD的中点G,连结PG,由VP-ACD=VA-PCD,能求出点B到面PCD的距离.
解答 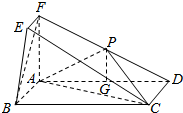 证明:(1)∵四边形ABCD为矩形,∴AD⊥AB,
证明:(1)∵四边形ABCD为矩形,∴AD⊥AB,
∵平面ABEF⊥平面ABCD,平面ABEF∩平面ABCD=AB,
AD?平面ABCD,又BF?平面ABEF,
∴AD⊥BF.
(2)取AD的中点G,连结PG,
∵∠BAF=90°,∴AF⊥AB,
又平面ABEF⊥平面ABCD,平面ABEF∩平面ABCD=AB,AF?平面ABEF,
∴AF⊥平面ABCD,
∵P、G分别为DF、AD的中点,
∴PG∥AF,∴PG⊥平面ABCD,
∵VP-ACD=VA-PCD,
∴$\frac{1}{3}{S}_{△ACD}•PG=\frac{1}{3}{S}_{△PCD}•{d}_{A-PCD}$,
∴dA-PCD=$\frac{{S}_{△ACD}•PG}{{S}_{△PCD}}$=$\frac{\frac{1}{2}×2×1×\frac{1}{2}}{\frac{1}{2}×1×\frac{\sqrt{5}}{2}}$=$\frac{2\sqrt{5}}{5}$,
∵AB∥面PCD,故dB-PCD=dA-PCD=$\frac{2\sqrt{5}}{5}$,
∴点B到面PCD的距离为$\frac{2\sqrt{5}}{5}$.
点评 本题考查异面直线垂直的证明,考查点到平面的距离的求法,是中档题,解题时要认真审题,注意等体积法的合理运用.

练习册系列答案
相关题目
17.f(x)=$\sqrt{1-{2^x}}$+$\frac{1}{{\sqrt{x+3}}}$的定义域为( )
| A. | (-∞,-3)∪(-3,0] | B. | (-∞,-3)∪(-3,1] | C. | (-3,0] | D. | (-3,1] |
8.设向量$\overrightarrow{AB}$=(2sinx,-1),$\overrightarrow{CD}$=(3,4),x∈(0,π),当|$\overrightarrow{AB}$|取最大值时,向量$\overrightarrow{AB}$在$\overrightarrow{CD}$方向上的投影为( )
| A. | $\frac{2}{5}$ | B. | $\frac{2}{5}$或-2 | C. | $\frac{3}{5}$ | D. | $\frac{3}{5}$或-2 |
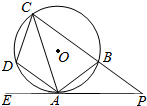 如图,四边形ABCD内接于⊙O,过点A作⊙O的切钱EP交CB 的延长线于P,己知∠PAB=25°.
如图,四边形ABCD内接于⊙O,过点A作⊙O的切钱EP交CB 的延长线于P,己知∠PAB=25°.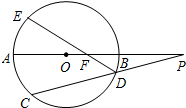 如图,圆O的直径AB的延长线与弦CD的延长线交于点P,E是圆O上的一点,弧$\widehat{AE}$与弧$\widehat{AC}$相等,ED与AB交于点F,AF>BF.
如图,圆O的直径AB的延长线与弦CD的延长线交于点P,E是圆O上的一点,弧$\widehat{AE}$与弧$\widehat{AC}$相等,ED与AB交于点F,AF>BF.