题目内容
3.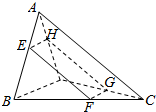 空间四边形ABCD的两条对棱AC,BD互相垂直,AC,BD的长分别为8和2,则平行四边形两条对棱的截面四边形EFGH在平移过程中,面积的最大值是4.
空间四边形ABCD的两条对棱AC,BD互相垂直,AC,BD的长分别为8和2,则平行四边形两条对棱的截面四边形EFGH在平移过程中,面积的最大值是4.
分析 假设EFGN是截面四边形,EFGN为平行四边形,设EN=x(0<x≤2),FE=y(0<y≤8),xy=S(S为所求面积),利用EN∥BD,可得$\frac{AN+ND}{AD}$=1=$\frac{x}{2}$+$\frac{y}{8}$,整理可得8=4x+y,利用基本不等式即可解得面积的最大值.
解答 解:如图,假设EFGN是截面四边形,EFGN为平行四边形;
设EN=x(0<x≤2),FE=y(0<y≤8),xy=S(S为所求面积);
由 EN∥BD,可得:$\frac{EN}{BD}=\frac{AN}{AD}$=$\frac{x}{2}$,$\frac{DN}{AD}$=$\frac{NG}{AC}$=$\frac{y}{8}$,
EN∥BD,可得:$\frac{EN}{BD}=\frac{AN}{AD}$=$\frac{x}{2}$,$\frac{DN}{AD}$=$\frac{NG}{AC}$=$\frac{y}{8}$,
两式相加,得:$\frac{AN+ND}{AD}$=1=$\frac{x}{2}$+$\frac{y}{8}$,
化简,得8=4x+y,
可得:8=4x+y≥2$\sqrt{4xy}$,(当且仅当2x=y时等号成立),解得:xy≤4,
解得:S=xy≤4.
故答案为:4.
点评 本题考查了直线与平面平行的性质,四边形取值范围的求法,是中档题,解题要认真审题,注意空间思维能力的培养.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
16.函数f(x)=-$\frac{1}{\sqrt{{x}^{2}+2x-3}}$的定义域是( )
| A. | [-3,1] | B. | (-3,1) | C. | (-∞,-3]∪[1,+∞) | D. | (-∞,-3)∪(1,+∞) |
17.f(x)=$\sqrt{1-{2^x}}$+$\frac{1}{{\sqrt{x+3}}}$的定义域为( )
| A. | (-∞,-3)∪(-3,0] | B. | (-∞,-3)∪(-3,1] | C. | (-3,0] | D. | (-3,1] |
18.命题“?x∈R,x2+5x<6”的否定是( )
| A. | ?x∈R,x2+5x≥6 | B. | ?x∈R,x2+5x=6 | C. | ?x0∈R,x02+5x0≥6 | D. | ?x∈R,x02+5x0<6 |
8.设向量$\overrightarrow{AB}$=(2sinx,-1),$\overrightarrow{CD}$=(3,4),x∈(0,π),当|$\overrightarrow{AB}$|取最大值时,向量$\overrightarrow{AB}$在$\overrightarrow{CD}$方向上的投影为( )
| A. | $\frac{2}{5}$ | B. | $\frac{2}{5}$或-2 | C. | $\frac{3}{5}$ | D. | $\frac{3}{5}$或-2 |
12.-150°的弧度数是( )
| A. | -$\frac{π}{3}$ | B. | -$\frac{5π}{6}$ | C. | -$\frac{2π}{3}$ | D. | $\frac{π}{6}$ |