题目内容
17．已知函数f（x）=lg$\frac{1+x}{1-x}$的定义域为集合A，函数g（x）=$\sqrt{3-x}$的定义域为集合B．（1）求集合A，B；
（2）求A∪B，（∁RA）∩（∁RB）．
分析 （1）求出f（x）的定义域确定出A，求出g（x）的定义域确定出B即可；
（2）由A与B，求出两集合的并集，找出A补集与B补集的交集即可．
解答 解：（1）由f（x）=lg$\frac{1+x}{1-x}$，得到$\frac{1+x}{1-x}$＞0，即（x+1）（x-1）＜0，
解得：-1＜x＜1，即A=（-1，1），
函数g（x）=$\sqrt{3-x}$，得到3-x≥0，即x≤3，
∴B=（-∞，3]；
（2）∵A=（-1，1），B=（-∞，3]，
∴A∪B=（-∞，3]，∁RA=（-∞，-1]∪[1，+∞），∁RB=（3，+∞），
则（∁RA）∩（∁RB）=（3，+∞）．
点评 此题考查了交、并、补集的混合运算，以及函数定义域及其求法，熟练掌握各自的定义是解本题的关键．
练习册系列答案
相关题目
8．设向量$\overrightarrow{AB}$=（2sinx，-1），$\overrightarrow{CD}$=（3，4），x∈（0，π），当|$\overrightarrow{AB}$|取最大值时，向量$\overrightarrow{AB}$在$\overrightarrow{CD}$方向上的投影为（ ）
| A． | $\frac{2}{5}$ | B． | $\frac{2}{5}$或-2 | C． | $\frac{3}{5}$ | D． | $\frac{3}{5}$或-2 |
5．由点P向圆x2+y2=1引两条切线PA、PB，A、B是切点，则$\overrightarrow{PA}$•$\overrightarrow{PB}$的最小值是（ ）
| A． | 6-4$\sqrt{2}$ | B． | 3-2$\sqrt{2}$ | C． | 2$\sqrt{2}$-3 | D． | 4$\sqrt{2}$-6 |
12．-150°的弧度数是（ ）
| A． | -$\frac{π}{3}$ | B． | -$\frac{5π}{6}$ | C． | -$\frac{2π}{3}$ | D． | $\frac{π}{6}$ |
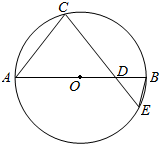如图，AB是圆O的直径，弦CE交AB于D，CD=4$\sqrt{2}$，DE=2$\sqrt{2}$，BD=2．