题目内容

设集合A={x|2a+1≤x≤3a-5}，B={x|3≤x≤22}，求能使A⊆A∩B成立的a值的集合．
考点：集合的包含关系判断及应用
专题：计算题,集合
分析：利用A⊆B，建立不等关系即可求解，注意当A=∅时，也成立．
解答： 解：若A=∅，即2a+1＞3a-5，解得a＜6时，满足A⊆B．
若A≠∅，即a≥6时，要使A⊆B成立，
则
2a+1≥3
3a-5≤22
，解得1≤a≤9，此时6≤a≤9．
综上a≤9．
点评：本题主要考查利用集合关系求参数取值问题，注意对集合A为空集时也成立，注意端点取值等号的取舍问题．
练习册系列答案
相关题目
椭圆
x2
4
+
y2
2
=1的离心率是（　　）
A、
2
4
B、
1
2
C、
2
2
D、
3
2
已知数列{an}满足a1=a，an+1=Sn+(-1)n，n∈N*，且{an+
2
3
(-1)n}是等比数列．
（1）求a的值；
（2）求出通项公式an；
（3）求证：
1
a3
+
1
a4
+…+
1
a2n-1
+
1
a2n
＜
3
2
．
试证明函数f（x）=-
1
x+1
在（-∞，-1）上是单调增函数．
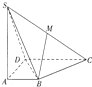四棱锥S-ABCD中，SA⊥平面ABCD，底面四边形ABCD为直角梯形，AB∥CD，AD⊥DC，SA=AD=DC=2，AB=1．
（Ⅰ）求证：平面SAD⊥平面SCD；
（Ⅱ）求二面角S-BC-D的余弦值；
（Ⅲ）M为SC中点，在四边形ABCD所在的平面内是否存在一点N，使得MN⊥平面SBD，若存在，求三角形ADN的面积；若不存在，请说明理由．
已知函数y=4cos2（2π-x）+4
3
cos（
π
2
-x）cosx-2，x∈R
（1）求函数的最小正周期；
（2）求函数的最大值及其相对应的x值；
（3）写出函数的单调增区间．
若数列{an}的前n项和为Sn，对任意正整数n都有6Sn=1-2an，记bn=log
1
2
an．
（Ⅰ）求a1，a2的值；
（Ⅱ）求数列{bn}的通项公式；
（Ⅲ）若cn+1-cn=bn，c1=0，求证：对任意n≥2，n∈N*都有
1
c2
+
1
c3
+…+
1
cn
＜
3
4
．
已知等比数列{an}的前n项和为Sn，且满足Sn=3n+k．
（1）求k的值及数列{an}的通项公式；
（2）若数列{bn}满足anbn=n，求数列{bn}的前n项和Tn．
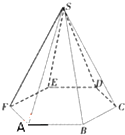正六棱锥的底面周长为24，侧面与底面所成角为60°．求：
（1）棱锥的高；
（2）侧棱长；
（3）侧棱与底面所成角的正切值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网