题目内容
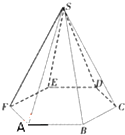 正六棱锥的底面周长为24,侧面与底面所成角为60°.求:
正六棱锥的底面周长为24,侧面与底面所成角为60°.求:(1)棱锥的高;
(2)侧棱长;
(3)侧棱与底面所成角的正切值.
考点:点、线、面间的距离计算,棱锥的结构特征
专题:计算题,空间位置关系与距离,空间角
分析:取BC中点H,连接SH,则SH⊥BC,则SO⊥底面
(1)∠SHO是侧面与底面所成角,可求棱锥的高;
(2)利用勾股定理,可求侧棱长;
(1)∠SBO是侧棱与底面所成角.
(1)∠SHO是侧面与底面所成角,可求棱锥的高;
(2)利用勾股定理,可求侧棱长;
(1)∠SBO是侧棱与底面所成角.
解答:
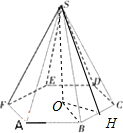 解:(1)正六棱锥底面周长为24,则底面边长为4,
解:(1)正六棱锥底面周长为24,则底面边长为4,
取BC中点H,连接SH,则SH⊥BC,
设O是正六边形的中心,连接SO,则SO⊥底面,
∵SH⊥BC,
∴∠SHO是侧面与底面所成角,
∴∠SHO=60°
∴SO=OHtan60°=4×
×
=6;
(2)Rt△SOB中,SO=6,OB=BC=4,
∴SB=
=2
;
(3)∵SO⊥底面,∴∠SBO是侧棱与底面所成角,
∴tan∠SBO=
=
 解:(1)正六棱锥底面周长为24,则底面边长为4,
解:(1)正六棱锥底面周长为24,则底面边长为4,取BC中点H,连接SH,则SH⊥BC,
设O是正六边形的中心,连接SO,则SO⊥底面,
∵SH⊥BC,
∴∠SHO是侧面与底面所成角,
∴∠SHO=60°
∴SO=OHtan60°=4×
| ||
| 2 |
| 3 |
(2)Rt△SOB中,SO=6,OB=BC=4,
∴SB=
| SO2+OB2 |
| 13 |
(3)∵SO⊥底面,∴∠SBO是侧棱与底面所成角,
∴tan∠SBO=
| SO |
| OB |
| 3 |
| 2 |
点评:本题考查点、线、面间的距离计算,考查线面角,考查学生的计算能力,比较基础.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目