题目内容
已知数列{an}为等差数列,且a5+a9=
,则tana7= .
| 8π |
| 3 |
考点:等差数列的性质
专题:等差数列与等比数列
分析:由等差数列的性质结合已知求得a7,取正切值得答案.
解答:
解:∵数列{an}为等差数列,且a5+a9=
,
∴2a7=a5+a9=
,则a7=
,
∴tana7=
=
.
故答案为:
.
| 8π |
| 3 |
∴2a7=a5+a9=
| 8π |
| 3 |
| 4π |
| 3 |
∴tana7=
| 4π |
| 3 |
| 3 |
故答案为:
| 3 |
点评:本题考查了等差数列的性质,考查了三角函数值的求法,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
(文科实验做)已知i为虚数单位,则(1+i)2012的值为( )
| A、22012 |
| B、-22012 |
| C、21006 |
| D、-21006 |
平移直线x-y+1=0使其与圆(x-2)2+(y-1)2=1相切,则平移的最短距离为( )
A、
| ||
B、2-
| ||
C、
| ||
D、
|
过直线l外的两点作与直线l平行的平面,这样的平面可作( )
| A、无数多个 |
| B、只有一个 |
| C、0个 |
| D、0个或一个或无数多个 |
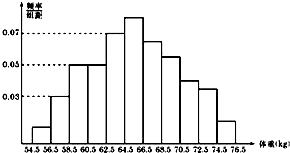 为了了解某地区高三学生的身体发育情况,抽查了该地区100名年龄为17.5岁~18岁的男生体重(kg),得到频率分布直方图如图:根据如图可得这100名学生中体重在[60.5,64.5]的学生人数是
为了了解某地区高三学生的身体发育情况,抽查了该地区100名年龄为17.5岁~18岁的男生体重(kg),得到频率分布直方图如图:根据如图可得这100名学生中体重在[60.5,64.5]的学生人数是 如图,在直三棱柱ABC-A1B1C1中,AB=AC=
如图,在直三棱柱ABC-A1B1C1中,AB=AC=