题目内容
已知椭圆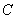 的中心在原点,焦点在
的中心在原点,焦点在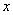 轴上,以两个焦点和短轴的两个端点为顶点的四边形是一个面积为
轴上,以两个焦点和短轴的两个端点为顶点的四边形是一个面积为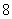 的正方形(记为
的正方形(记为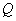 )
)
(1)求椭圆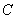 的方程
的方程
(2)设点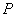 是直线
是直线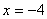 与
与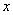 轴的交点,过点
轴的交点,过点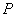 的直线
的直线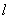 与椭圆
与椭圆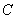 相交于
相交于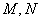 两点,当线段
两点,当线段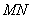 的中点落在正方形
的中点落在正方形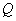 内(包括边界)时,求直线
内(包括边界)时,求直线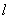 斜率的取值范围
斜率的取值范围
解: (Ⅰ)依题意,设椭圆C的方程为=1(a>b>0),焦距为2c,
由题设条件知,a2=8,b=c, 所以b2=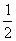 a2=4
a2=4
故椭圆C的方程为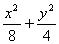 =1 (4分)
=1 (4分)
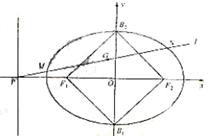 (Ⅱ)椭圆C的左准线方程为x=-4,所以点P的坐标为(-4,0),
(Ⅱ)椭圆C的左准线方程为x=-4,所以点P的坐标为(-4,0),
显然直线l的斜率k存在,所以直线的方程为y=k(x+4)。
如图,设点M,N的坐标分别为(x1,y1),(x2,y2),线段MN的
中点为G(x0,y0),
由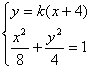
得(1+2k2)x2+16k2x+32k2-8=0 ① (6分)
由D=(16k2)2-4(1+2k2)(32k2-8)>0
解得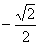 <k<
<k<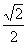 ② (7分)
② (7分)
因为x1,x2是方程①的两根,所以x1+x2=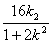 ,
,
于是x0=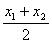 =
=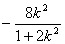 ,y0=k(x0+4)=
,y0=k(x0+4)= (8分)
(8分)
∵x0=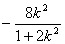 ≤0,所以点G不可能在y轴的右边. (9分)
≤0,所以点G不可能在y轴的右边. (9分)
又直线F1B2,F1B1方程分别为y=x+2,y=-x-2
所以点G在正方形Q内(包括边界)的充要条件为
 即
即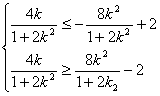 (10分)
(10分)
解得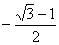 ≤k≤
≤k≤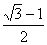 ,此时②也成立. (12分)
,此时②也成立. (12分)
故直线l斜率的取值范围是[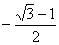 ,
,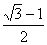 ]. (13分)
]. (13分)

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
 上的任意一点,若∠PF1F2=α,∠PF2F1=β,且cosα=
上的任意一点,若∠PF1F2=α,∠PF2F1=β,且cosα= ,sin(α+β)=
,sin(α+β)= ,则此椭圆的离心率为 .
,则此椭圆的离心率为 . 的渐近线与圆
的渐近线与圆 有公共点,则该双曲线离心率的取值范围是__________.
有公共点,则该双曲线离心率的取值范围是__________. 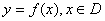 ,若存在常数
,若存在常数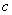 ,对任意
,对任意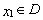 ,存在唯一
,存在唯一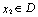 的,使得
的,使得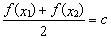 ,则称函数
,则称函数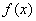 在
在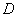 上的均值为
上的均值为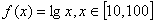 ,则函数
,则函数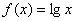 在
在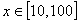 上的均值为。
上的均值为。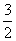 B.
B. 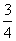 C.
C. 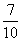 D.
D. 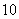
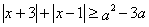 对任意实数
对任意实数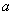 的取值范围为_________________
的取值范围为_________________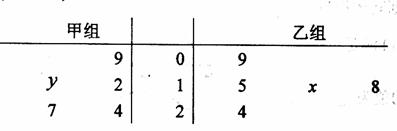
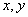 的值分别为
的值分别为
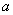 和
和 ,定义运算“
,定义运算“ ”:
”: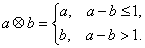 设函数
设函数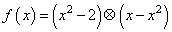 ,
,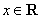 .若函数
.若函数 的图象与
的图象与 轴恰有两个公共点,则实数
轴恰有两个公共点,则实数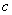 的取值范围是( ).
的取值范围是( ).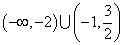 B.
B.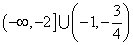
 D.
D.
 中:
中: ,则
,则 .
.