题目内容
曲线f(x)=x2+x+1在点(0,1)处的切线方程为( )
| A、x+y+1=0 |
| B、x+y-1=0 |
| C、x-y+1=0 |
| D、x-y-1=0 |
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用
分析:根据导数的几何意义求出f(x)=x2+x+1在点(0,1)的切线的斜率f′(0),再由点斜式写出切线方程即可.
解答:
解:∵f(x)=x2+x+1,
∴f′(x)=2x+1
∴根据导数的几何意义可得曲线f(x)=x2+x+1在(0,1)处的切线的斜率为f′(0)=1
∴曲线f(x)=x2+x+1在(0,1)处的切线方程为y-1=f′(0)(x-0)即x-y+1=0.
故选:C.
∴f′(x)=2x+1
∴根据导数的几何意义可得曲线f(x)=x2+x+1在(0,1)处的切线的斜率为f′(0)=1
∴曲线f(x)=x2+x+1在(0,1)处的切线方程为y-1=f′(0)(x-0)即x-y+1=0.
故选:C.
点评:本题主要考查了利用导数的几何意义求出曲线在某点处的切线方程,解题的关键是求出曲线f(x)=x2+x+1在点(0,1)的切线的斜率.

练习册系列答案
相关题目
若抛物线y2=x上一点P到准线的距离等于它到顶点的距离,则点P到x轴的距离为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数y=2sinx(0<x≤
)的值域是( )
| 2π |
| 3 |
A、(0,
| ||
B、[-
| ||
| C、[-2,2] | ||
| D、(0,2] |
已知f(x)=cosx,则f′(
)=( )
| π |
| 2 |
| A、1 | B、0 | C、-1 | D、2 |
如图是“集合”的知识结构图,如果要加入“子集”,则应放在( )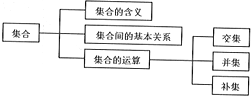

| A、“集合的含义”的下位 |
| B、“集合间的基本关系”的下位 |
| C、“交集”的下位 |
| D、“集合的运算”的下位 |
直线l过点P(1,2)且倾斜角是直线x-2y=0倾斜角的2倍,则直线l的方程是( )
| A、3x-4y+5=0 |
| B、x-y=0 |
| C、4x-3y+2=0 |
| D、2x-y=0 |
若函数y=2cos2(ωx-
)(ω>0)的最小正周期T=
,则ω=( )
| π |
| 2 |
| π |
| 2 |
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
直线
+
=1与两坐标轴围成的三角形的周长为( )
| x |
| 3 |
| y |
| 4 |
| A、6 | B、7 | C、12 | D、14 |