题目内容
设y=loga
的定义域为[s,t],值域为[loga(at-a),loga(as-a)].
(1)求证:s>3;
(2)求a的取值范围.
| x-3 |
| x+3 |
(1)求证:s>3;
(2)求a的取值范围.
考点:对数函数图象与性质的综合应用
专题:计算题,函数的性质及应用
分析:(1)由题意可得
>0,再由loga
=loga(as-a),求证s>3;
(2)由题意可化为as2+(2a-1)s+3-3a=0有两个不相同的实根,从而求a的取值范围.
| s-3 |
| s+3 |
| s-3 |
| s+3 |
(2)由题意可化为as2+(2a-1)s+3-3a=0有两个不相同的实根,从而求a的取值范围.
解答:
解:(1)证明:由题意,
>0,
∴s>3或s<-3,
根据值域和定义域可知函数为减函数,
∴0<a<1,
∴loga
=loga(as-a),则
=as-a=a(s-1)>0,
∴s>1,
∴s>3.
(2).由
=as-a可化为as2+(2a-1)s+3-3a=0,
由已知可知,as2+(2a-1)s+3-3a=0的两根一个是s,另一个是,
∴(2a-1)2-4a(3-3a)>0,
∴0<a<
或
<a<1.
| s-3 |
| s+3 |
∴s>3或s<-3,
根据值域和定义域可知函数为减函数,
∴0<a<1,
∴loga
| s-3 |
| s+3 |
| s-3 |
| s+3 |
∴s>1,
∴s>3.
(2).由
| s-3 |
| s+3 |
由已知可知,as2+(2a-1)s+3-3a=0的两根一个是s,另一个是,
∴(2a-1)2-4a(3-3a)>0,
∴0<a<
2-
| ||
| 4 |
2+
| ||
| 4 |
点评:本题考查了对数函数的图象及性质与其应用,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
圆x2+y2-6x=0的圆心恰为y2=2px(p>0)的焦点,则p的值为( )
| A、4 | B、5 | C、6 | D、7 |
种植某种树苗,成活率为0.9,现采用随机模拟的方法估计该树苗种植5棵恰好4棵成活的概率,先由计算机产生0到9之间取整数值的随机数,指定1至9的数字代表成活,0代表不成活,再以每5个随机数为一组代表5次种植的结果.经随机模拟产生如下30组随机数:
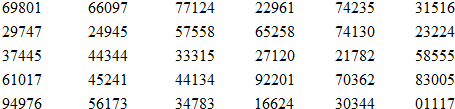
据此估计,该树苗种植5棵恰好4棵成活的概率为( )
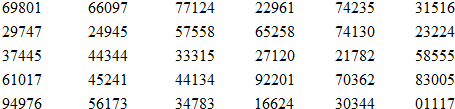
据此估计,该树苗种植5棵恰好4棵成活的概率为( )
| A、0.30 | B、0.35 |
| C、0.40 | D、0.50 |
一物体以速度v(t)=3t2-2t+3做直线运动,它在t=0和t=3这段时间内的位移是( )
| A、9 | B、18 | C、27 | D、36 |