题目内容
7.函数$y=\frac{1}{{\sqrt{{{log}_2}({4x-1})}}}$的定义域为( )| A. | $(0,\frac{1}{2})$ | B. | $(\frac{3}{4},+∞)$ | C. | $(\frac{1}{2},+∞)$ | D. | ($\frac{3}{4}$,1) |
分析 由分母中根式内部的代数式大于0,求解对数不等式得答案.
解答 解:要使原函数有意义,则log2(4x-1)>0,
即4x-1>1,得x$>\frac{1}{2}$.
∴函数$y=\frac{1}{{\sqrt{{{log}_2}({4x-1})}}}$的定义域为$(\frac{1}{2},+∞)$.
故选:C.
点评 本题考查函数的定义域及其求法,是基础的计算题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.已知sinα-cosα=$\frac{1}{5}$,则cos2($\frac{5π}{4}$-α)=( )
| A. | $\frac{1}{50}$ | B. | $\frac{13}{50}$ | C. | $\frac{37}{50}$ | D. | $\frac{49}{50}$ |
12.实数x,y满足$\left\{\begin{array}{l}{x+2y-3≤0}\\{x+3y-3≥0}\\{y≤1}\end{array}\right.$,则z=y-x的最大值是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
16.某防疫站对学生进行身体健康调查,欲采用分层抽样的办法抽取样本.某中学生共有学生2000名,抽取了一个容量为200的样本,样本中男生103人,则该中学生共有女生( )
| A. | 1030人 | B. | 97人 | C. | 950人 | D. | 970人 |
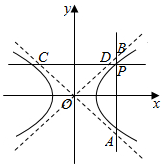 已知P为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1上的任意一点,过P作x轴的垂线,分别交双曲线的两条渐近线于A,B两点,过P作y轴的垂线,分别交双曲线的两条渐近线于C,D两点.求证:|PA|•|PB|+|PC|•|PD|为定值.
已知P为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1上的任意一点,过P作x轴的垂线,分别交双曲线的两条渐近线于A,B两点,过P作y轴的垂线,分别交双曲线的两条渐近线于C,D两点.求证:|PA|•|PB|+|PC|•|PD|为定值. 如图所示的阴影部分是由底边长为1,高为1的等腰三角形及宽为1,长分别为2和3的两矩形所构成.设函数S=S(a)(a≥0)是图中阴影部分介于平行线y=0及y=a之间的那一部分的面积,则函数S(a)的图象大致为( )
如图所示的阴影部分是由底边长为1,高为1的等腰三角形及宽为1,长分别为2和3的两矩形所构成.设函数S=S(a)(a≥0)是图中阴影部分介于平行线y=0及y=a之间的那一部分的面积,则函数S(a)的图象大致为( )


