题目内容
2.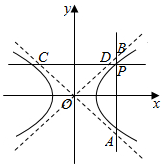 已知P为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1上的任意一点,过P作x轴的垂线,分别交双曲线的两条渐近线于A,B两点,过P作y轴的垂线,分别交双曲线的两条渐近线于C,D两点.求证:|PA|•|PB|+|PC|•|PD|为定值.
已知P为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1上的任意一点,过P作x轴的垂线,分别交双曲线的两条渐近线于A,B两点,过P作y轴的垂线,分别交双曲线的两条渐近线于C,D两点.求证:|PA|•|PB|+|PC|•|PD|为定值.
分析 设P(m,n),可得$\frac{{m}^{2}}{{a}^{2}}$-$\frac{{n}^{2}}{{b}^{2}}$=1,即为b2m2-a2n2=a2b2,求出双曲线的渐近线方程,令x=m,y=n,分别求得A,B,C,D的坐标,运用两点的距离公式化简整理,即可得证.
解答 证明:设P(m,n),可得$\frac{{m}^{2}}{{a}^{2}}$-$\frac{{n}^{2}}{{b}^{2}}$=1,
即为b2m2-a2n2=a2b2,
双曲线的渐近线方程为y=±$\frac{b}{a}$x,
由x=m,可得y=±$\frac{bm}{a}$,
即有A(m,$\frac{bm}{a}$),B(m,-$\frac{bm}{a}$),
由y=n,可得x=±$\frac{an}{b}$,
即有C($\frac{an}{b}$,n),D(-$\frac{an}{b}$,n),
可得|PA|•|PB|+|PC|•|PD|=|n-$\frac{bm}{a}$|•|n+$\frac{bm}{a}$|+|m-$\frac{an}{b}$|•|m+$\frac{an}{b}$|
=|n2-$\frac{{b}^{2}{m}^{2}}{{a}^{2}}$|+|m2-$\frac{{a}^{2}{n}^{2}}{{b}^{2}}$|=$\frac{{a}^{2}{b}^{2}}{{a}^{2}}$+$\frac{{a}^{2}{b}^{2}}{{b}^{2}}$=a2+b2.即为定值.
点评 本题考查双曲线的方程和性质,主要是渐近线方程的运用,考查化简整理的运算能力,属于中档题.

练习册系列答案
相关题目
17.下列有关命题的说法正确的是( )
| A. | “若x≠a且x≠b,则x2-(a+b)x+ab≠0”的否命题为:“若x=a且x=b,则x2-(a+b)x+ab=0” | |
| B. | “x=-1”是“x2-5x-6=0”的根的逆命题是真命题 | |
| C. | 命题“?x∈R,使得x2+x+1<0”的否定是:“?x∈R,均有x2+x+1<0” | |
| D. | 命题“若x=y,则sinx=siny”的逆否命题为真命题 |
7.函数$y=\frac{1}{{\sqrt{{{log}_2}({4x-1})}}}$的定义域为( )
| A. | $(0,\frac{1}{2})$ | B. | $(\frac{3}{4},+∞)$ | C. | $(\frac{1}{2},+∞)$ | D. | ($\frac{3}{4}$,1) |
14.某学校高三年级有学生500人,其中男生300人,女生200人,为了研究学生的数学成绩是否与性别有关,现采用分层抽样的方法,从中抽取了100名学生,先统计了他们期中考试的数学分数,然后按性别分为男、女两组,再将两组学生的分数分成5组:[100,110),[110,120),[120,130),[130,140),[140,150]分别加以统计,得到如图所示的频率分布直方图.
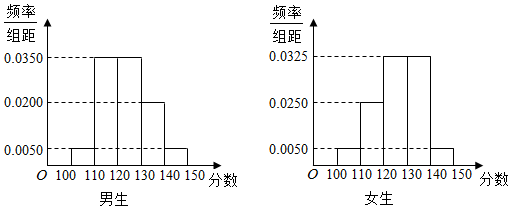
(1)从样本中分数小于110分的学生中随机抽取2人,求两人恰好为一男一女的概率;
(2)若规定分数不小于130分的学生为“数学尖子生”,请你根据已知条件完成2×2列联表,并判断是否有90%的把握认为“数学尖子生与性别有关”?
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.

(1)从样本中分数小于110分的学生中随机抽取2人,求两人恰好为一男一女的概率;
(2)若规定分数不小于130分的学生为“数学尖子生”,请你根据已知条件完成2×2列联表,并判断是否有90%的把握认为“数学尖子生与性别有关”?
| P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 6.635 | 10.828 |
11.若实数x,y满足$\left\{\begin{array}{l}x+y-3≥0\\ x-y-3≤0\\ 0≤y≤1\end{array}\right.$,则$z=\frac{2x+y}{x+y}$的最小值为( )
| A. | $\frac{5}{3}$ | B. | 2 | C. | $\frac{3}{5}$ | D. | $\frac{1}{2}$ |