题目内容
在△ABC中，A=30°，AB=2，BC=1，则AC= ．
考点：余弦定理
专题：解三角形
分析：利用余弦定理列出关系式，把a，c，cosA的值代入求出b的值，即为AC的长．
解答：
解：∵在△ABC中，A=30°，AB=c=2，BC=a=1，
∴由余弦定理得：a2=b2+c2-2bccosA，即1=b2+4-2
b，
解得：b=
，
则AC=b=
．
故答案为：
∴由余弦定理得：a2=b2+c2-2bccosA，即1=b2+4-2
| 3 |
解得：b=
| 3 |
则AC=b=
| 3 |
故答案为：
| 3 |
点评：此题考查了余弦定理，以及特殊角的三角函数值，熟练掌握余弦定理是解本题的关键．
练习册系列答案
相关题目
已知数列{an}中，a1=2，an+1=an+2n（n∈N*），则a100的值是（ ）
| A、9900 | B、9902 |
| C、9904 | D、11000 |
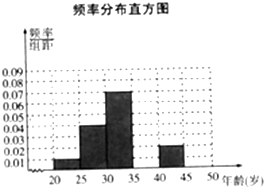为调查市民对汽车品牌的认可度，在秋季车展上，从有意购车的500名市民中，随机抽样100名市民，按年龄情况进行统计的频率分布表Ⅰ和频率分布直方图2